College Algebra Final
SHORT ANSWER.
1. Use the graph of the given function to determine each of the following.
Where applicable, use
interval notation.
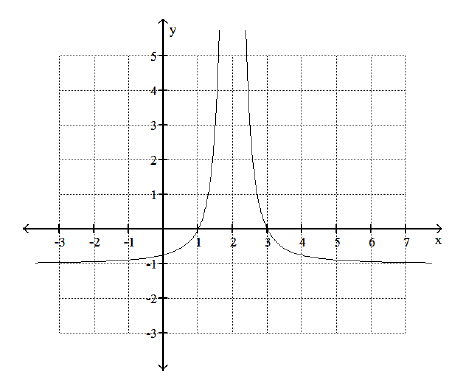
a) the domain of f
b) the value of the zero(s) of f
c) the approximate value of f(0)
d) the equation of the vertical asymptote
e) the number f(x) approaches as x approaches infinity
f) interval(s) on which f is increasing
g) values of x for which f(x) < 0
h) the value(s) of x for which f(x) = 3
i) the range of f
2. Solve.
A school has just purchased new computer equipment for $22,000.00. The graph
shows the depreciation of the equipment over 5 years. The point (0, 22,000)
represents the purchase price and the point (5, 0) represents when the equipment
will be replaced.
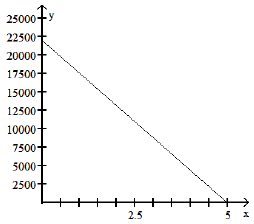
a) Write a linear equation in slope-intercept form that models the value of the equipment, y, x years after purchase.
b) Use the model to predict the value of the equipment after 4 years.
c) What is the slope of the line whose equation you found in part (a)? Interpret
the slope
verbally.
3. Solve.
The perimeter of a rectangle is 48 feet. If x and y are the length and width of
the rectangle, 2x + 2y = 48.
a) Write y in terms of x.
b) Write the area of the rectangle as a function of x.
c) Graph the area function.
d) What is the maximum possible area?
4. Solve.
Medical research indicates that the risk of having a car accident increases
exponentially as the concentration of alcohol in the blood increases. The risk
is modeled by R = 6e12.77x where x is the blood alcohol concentration and R,
given as a percent, is the risk of having a car accident.
a) In many states it is illegal to drive with a blood alcohol concentration of
0.08 or more. What is the risk of having a car accident with a blood alcohol
concentration of 0.08?
b) What blood alcohol concentration corresponds to a 20% risk of a car accident?
c. Is the risk of having a car accident ever 0 with this model?
d) What is the risk if a driver's blood alcohol concentration is zero?


