Discrete Structure Homework: Logic II

1. (10) (1.6: 6) Use a direct proof to show that the product of two odd integers is
odd.

Let a, b be odd integers. Then we can write a = 2x + 1 and b = 2y + 1 for
some integers x, y. Multiplying a and b gives:

ab = (2x + 1)(2y + 1)
= 4xy + 2(x + y) + 1
= 2(2xy + x + y) + 1

Therefore the product of two odd integers is odd.

2. (1.6: 12) Prove or disprove that the product of a nonzero rational number and
an irrational number is irrational.

By contradiction: Let x ∈ Q \ {0} and y ∈ R \ Q. Assume that xy = z ∈ Q.
Then there exists a, b, c, d ∈ Z such that 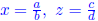Then

xy = z
y = zx^-1

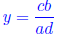
y ∈ Q

Since y ∈ R\Q, this contradicts our assumption and the product of a nonzero
rational number and and irrational number is irrational.

3. (1.6: 16) Prove that if m and n are integers and mn is even then m is even or n
is even.

Proof by contradiction: Assume both m and n are odd and mn is even. Then
from the definition of odd integers there exists 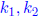∈ Z such that
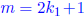
and 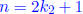. Then 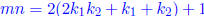, which is an odd integer.
Since mn is even, this contradicts our assumption and at least one of m or n
is even.

4. (1.6: 20)Prove the proposition P(1), where P(n) is the proposition “If n is a
positive integer, then n² ≥ n”. What kind of proof did you use?

P(1) states that 1² ≥ 1. Since 1² = 1, P(1) is true. Direct proof.

5. (15) (1.6: 28) Prove the m² = n² if and only if m = n or m = -n.

If m = n or m = -n, then m² = (±n)² = n². If m² = n², then

0 = m² - n²
= (m - n)(m + n)

Since ab = 0 if and only if a = 0 or b = 0, therefore either m - n = 0, and
m = n or m + n = 0, and m = -n. (NOTE: poorly worded problem as it
doesn't state the domain of m, n. If m, n ∈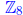, for example, and m = 2, n = 6,
then m² ≡ 4 mod 8 and n² = 36 = 8(4) + 4 ≡ 4 mod 8)

6. (1.7: 2) Prove that there are no positive perfect cubes less than 1000 that are
the sum of the cubes of two positive integers.

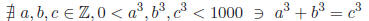
Proof by exhaustion: The only possible values for a, b, c are the integers
1, 2, . . . , 9. The table below gives a, a³, then c³-a³, for all c, a pairs whose result
is greater than zero. None of these produces a perfect cube (b³), therefore
no a, b, c ∈ Z, a, b, c > 0 exists with a³ + b³ = c³ and c < 1000.

7. (10) (1.7: 6) Prove that there is a positive integer that equals the sum of the positive
integers not exceeding it. Is the prove constructive or non-constructive.

1 = 1, therefore this hypothesis is true. This is a constructive proof.

8. (1.7: 8) Prove that either (2 × 10⁵⁰⁰ + 15) or (2 × 10⁵⁰⁰ + 16) is not a perfect
square. Is the proof constructive or non-constructive.

Proof by contradiction: Let a = 2 × 10⁵⁰⁰ + 15 and b = a + 1. Assume
both a, b are perfect squares 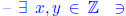a = x², b = y². Therefore
b - a = y² - x² = 1. But y² - x² = (y - x)(y + x) = 1, and y - x, y + x ∈ Z.
Therefore y - x = y + x and equals either 1 or -1. But this implies that
-x = x or x = 0, a = 0 which contradicts the definition of a. Therefore both
a and b are not perfect squares

9. (1.7: 12) Prove or disprove that if a, b ∈ Q, then a^b ∈ Q.

Proof by counter example: Let a = 2, 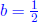. We know that 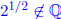, therefore
a, b ∈ Q does not imply that a^b ∈ Q.

10. (1.7: 14) Show that if a, b, c ∈ R and a ≠ 0, then there is a unique solution x
of the equation ax + b = c.

Direct proof: Since a ≠ 0, 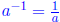, and x = (c-b)a^-1. If x ∈ R is a solution
to ax + b = c, then ax = c - b and x = (c - b)/a, therefore the solution is
unique.

11. (15) (1.7: 28) Prove that there are no solutions x, y ∈ Z to the equation 2x² +
5y² = 14.

Proof by contradiction: If x, y ∈ Z and 2x² + 5y² = 14 then WLOG we can
assume x, y ≥ 0. We also know x, y ≠ 0 since no x or y exists such that
2x² = 14 or 5y² = 14. Thus 0 < x < 3 and 0 < y < 2, and y = 1. This
implies 2x² = 14 - 5 = 9. But 9 is odd and 2x² is even, therefore no x, y ∈ Z
exist 5y² = 14 - 2x².

12. (1.7: 36) Prove or disprove that if you have an 8 gallon jug (8G) of water and
a 5G and 3G empty jugs, then you can measure 4G by successively pouring
some of or all of the water in one jug into another.

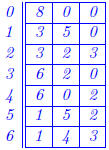	Start
	Pour 5g from 8G to 5G
	Pour 3g from 5G to 3G
	Pour 3g from 3G to 8G
	Pour 2g from 5G to 3G
	Pour 5g from 8G to 5G
	Pour 1g from 5G to 3G