Inverse Functions
Definition 1.1. We will define another special type
of composition function,
called the inverse function. A function g is called the inverse function
of f
if
• f (g (x)) = x for all x in the domain of g
• g (f (x)) = x for all x in the domain of f
Be careful to notice that for functions to be inverses, both criteria
must be
satisfied.
Example 1.2. Let f (x) = 3x + 1 and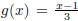 
. Notice that f and g are
inverse functions:
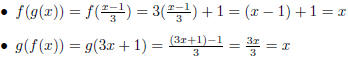
Since f (g (x)) = x = g (f (x)) for all x, they must be
inverse functions.
Example 1.3. Let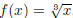 
and
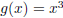. Notice that f and g are inverse
functions:
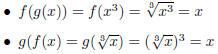
Since f (g (x)) = g (f (x)) for all x, they must be
inverse functions.
Example 1.4. Let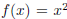 
, and
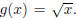What happens to the criteria
for inverses?
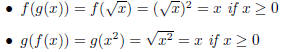
Thus, f and g are not inverse function, if we are
using all of R as our domain.
The are inverses if we only use [0,∞) as our domain.
Item 1.5. Really, all an inverse function does, is answer the question,
“what x
value will give me a y value of --?” Inverses switch the input and the output of a
function, since we HAVE the y value, and WANT the x value, as opposed to the
usual case. Since this switching of input and output is what inverse functions
do, we can use this tool to actually FIND the inverse of a function.
Example 1.6. Find the inverse function for f (x) = 7x + 2. To do so, we
will
make use of the same procedure we used to find the range of a function: we will
solve for x in terms of y:
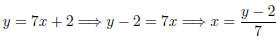
Since inverse functions switch the input and output, change y and x:
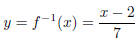
is the inverse of f.
Example 1.7. Use the same procedure to find the inverses for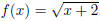 
,
and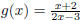 
.
Item 1.8. Notice that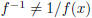
. Use f (x) = 2x
+ 1 as a counterexample.
Item 1.9. If there the ordered pair (4, 5) is on the graph of f (x), then
the
ordered pair (5, 4) is on the graph of f -1(x), since inverses switch input and
output. If we keep plotting points on f and on f -1, we’ll notice that f -1 is
just
a reflection of f over the line y − x. As examples, plot the following graphs:
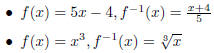
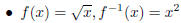on the right
half-plane, [0,∞)
Definition 1.10. A function is said to be one to one if
every y value is the
image of exactly one x value
Item 1.11. If we reflect a vertical line, which will tell us if a graph is a
function
(remember the vertical line test gives us a function if the line hits the graph
at only one point), about the line y = x, since that’s what inverses do, we get
a horizontal line. So if an inverse is a function, then reflection across the
line
y = x gives us a horizontal line crossing the original function exactly once.
For examples, graph y = x2, which fails the test, and y = x3, which passes the
horizontal line test.
Example 1.12. Show algebraically that y = 7x + 2 has an inverse. Assume
that there are two values, a and b that have the same y value:
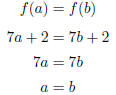
So if two numbers give us the same y value, they have to
be the same. Thus,
7x + 2 has an inverse.
Example 1.13. Show algebraically that y = x2 +2 has no inverse. Notice that
f(2) = 6 = f(−2). So there are two x values that give the same y values, and
x2 + 2 has no inverse.
Item 1.14. Please do the following problems on pages 238ff. to turn in:
1, 5, 9, 13, 23, 25, 27, 29, 31, 33