Math 23b Final Review
Below you will find the list of some of the topics which may appear on the
exam, and some
suggestions for preparation. References are made to the corresponding
pages/statements
in the textbook. The final exam will cover Chapters 1-4, 13-14 and the first two
sections
of Chapter 15.
1. Review all the homework assignments, quizzes, and the midterm exam.
2. Know the definitions of
(a) basic operations with sets (union, intersection, complement, containment and
equality
of sets, Cartesian product, power set)
(b) a function, injective, surjective, and bijective functions, composition of
functions, in-
verse of a function, a graph of a function, inverse images and level sets
(c) bounded subsets of R and bounded real-valued functions,
increasing/decreasing real-
valued functions
(d) logical operations and quantifiers
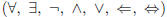
(e) finite, infinite, countable sets, the size of a finite set, two sets having
the same cardinality
( f ) upper/lower and least upper/greatest lower bounds of subsets of R
(g) limits of sequences, convergent sequences
(h) the canonical k-ary expansion of a real number
( i ) Cauchy sequences, a subsequence of a sequence
( j ) infinite series, partial sums of a series, convergent/divergent series,
geometric series,
harmonic series
(k) limits of functions, continuous functions
3. Be familiar with the following:
(a) the arithmetic-geometric mean inequality, the triangle inequality (4-5)
(b) properties of the real number system (16-17, you do not have to remember
which
properties are axioms and which are propositions)
(c) direct, contrapositive and \by contradiction" proof techniques (35-39)
(d) principles of induction (51-57) and strong induction (63-64), well-ordering
property of
N and the method of descent (64-66)
(e) the fact that two finite sets have the same number of elements (size) if and
only if there
exists a bijection between them
( f ) the fact that if two functions are injective/surjective/bijective, then so
is their composition (Proposition 4.30, proved in class)
(g) that two finite sets have the same number of elements (size) if and only if
there exists
a bijection between them (Proposition 4.37, proved in class)
(h) examples of countable sets discussed in Chapter 4 and in class (89-90)
( i ) the Completeness Axiom (256-257), the Archimedean Property (258)
( j ) the Monotone Convergence Theorem (261)
(k) uncountability of the set of real numbers (266)
( l ) arithmetic properties of limits, the Squeeze Theorem for limits (272-274)
(m) the Bolzano-Weierstrass Theorem and the method of bisection, Cauchy
Convergence
Criterion (276-279)
(n) a formula for the sum of geometric series (280), the divergence of harmonic
series (282)
(o) comparison/ratio/root tests for series (282-284)
(p) the equivalence of de nitions of limit and sequential limit of functions
(294-296) and
its consequences (296-298)
(q) the Intermediate Value Theorem and its applications (299-300)
And here are some sample problems:
4. Using the triangle inequality, prove that if x and y are real numbers then
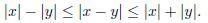
5. Using logical connectives, quantifiers, and the usual symbols of
mathematics (but no words)
write down an expression without negation signs that means "the sequence <a>
does not
converge." For example,
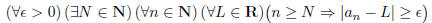
has the right form, though it is not correct.
6. Let A,B be two nonempty sets and let f : A -> B be a surjective function.
Which of the
following must be true? Find counterexamples to statements which are not true.
(a) For every x ∈A there is at least one y
∈B such that f(x) = y.
(b) For every x ∈A there is at most one y
∈B such that f(x) = y.
(c) For every y ∈B there is at least one x
∈A such that f(x) = y.
(d) For every y ∈B there is at most one x
∈A such that f(x) = y.
7. A sequence <a> is defined by
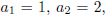and
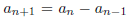for n > 2. Prove by
induction that for all
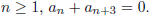
8. Define a sequence <b> by b1 = 1 and
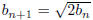for n > 1. Prove by induction that for
all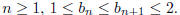 
Does this sequence converge? what is its limit?
9. Let A be a nonempty finite set, and let F be the set of
all functions from A to N. Prove
that F is countable.
0. Let A,B be two nonempty subsets of R such that
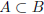and B is bounded above. Prove
that A is also bounded above and supA≤supB.
11. Prove that the following statement is not true: For
any sequence <a>, if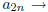 
L then
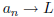. Is the converse true?
12. Let <a> and <b> be infinite sequences of real numbers
such that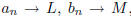 
and
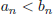for all n. Prove that L≤M. [Hint: Proof by
contradiction.]
13. Using only the definition of a Cauchy sequence, prove
that the sequence <b> given by
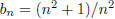is Cauchy.
14. Does there exist
(a) a Cauchy sequence that is not monotone?
(b) a monotone sequence that is not Cauchy?
(c) a Cauchy sequence with a divergent subsequence?
(d) an unbounded sequence containing a sequence which is Cauchy?
Give examples if yes, provide a justification if no.
15. Using only the definition of a limit prove that if <a>
converges to L and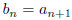 
for all
n then <b> converges to L.
16. Let <a> be a sequence with
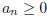for all n and such that
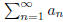converges. Prove that 
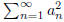also converges.
17. Using only the definition of continuity, prove that
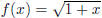is continuous at x = 3.
18. Let f and g be continuous on (-1, 1) and suppose that
f(x) < g(x) for all 0 < x < 1.
Prove that f(0)≤g(0). Show that f(0) < g(0) might be false.