Math 3C Review Sheet
1 Functions in general
1. Ways of expressing: table, graph, formula, words
2. Input and output; domain and range. Interval notation.
3. Describing change of a function: average rate of change, increasing and
decreasing functions, concavity
4. Short run behavior: zeros, vertical asymptotes, holes, etc.
5. Long run behavior: horizontal asymptotes, dominance, long-run similarity of
functions
6. Periodic functions: period, amplitude, midline. Trigonometric functions as
examples. See below.
7. Piecewise defined functions. Example: absolute value function f(x) = |x|.
8. Operations on functions
(a) Composition f(g(x))
(b) Arithmetic combinations f(x) + g(x), f(x)g(x) etc.
(c) Inverse function f-1(y): find input for a given output
i. Horizontal line test for invertible functions
ii. Finding formula by solving y = f(x) for x
iii. Graph: reflection about diagonal line y = x, domain and range swap
iv. Composition of inverses: f(f-1(x)) = f-1(f(x)) = x
v. Examples: see below.
(d) Transformations of functions
i. Inside and outside changes; horizontal and vertical
ii. Shifts, stretches/compressions, reflections/flips.
iii. Even and odd functions
2 Specific families of functions
1. Linear functions
(a) Constant rate of change (slope). Graph: straight line.
(b) Formulas for linear functions: slope-intercept form y = mx+b, pointslope
form y − y0 = m(x - x0), standard form Ax + By + C = 0.
(c) Solving linear equations and linear systems. Parallel and perpendicular
lines.
2. Exponential and logarithmic functions
(a) Properties of exponents and logarithms: log(ab) = log a + log b, etc.
(b) Graphs and general shape. Example of inverse functions
(c) Solving equations using/involving exponents and logarithms. Finding formulas
for exponential functions.
(d) Applications: interest, population growth, radioactive decay, logarithmic
scales, etc.
3. Trigonometric functions: sin t, cos t, tan t
(a) Definitions in terms of unit circle. Special angles
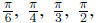etc. Symmetry properties, even and odd functions.
(b) Radian measure and arc length
(c) Sinusoidal functions: transformations of sin t and cos t. Effect on period,
amplitude, midline, phase shift.
(d) Trigonometric identities: Pythagorean identity, double angle formula, phase
shifts by
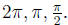
(e) Inverse trigonometric functions: arcsin t or sin-1 t, etc. Restriction of
domain to avoid failure of horizontal line test.
(f) Applications
i. Solving right triangles: adjacent/opposite/hypotenuse
ii. Solving non-right triangles: law of sines, law of cosines
iii. Modeling periodic behavior
4. Power functions f(x) = kxp.
(a) Shape of graph for various values of p
(b) Negative p: vertical and horizontal asymptotes
(c) Even and odd functions
(d) Finding formulas using logarithms
5. Quadratic functions: f(x) = ax^2 + bx + c
(a) Graph: parabola. Concave up or down.
(b) Finding zeros: factoring, quadratic formula
(c) Finding vertex: vertex form (transformation of g(x) = x^2), completing the
square.
6. Polynomials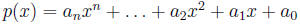 
(a) Sum of power functions. Standard form, leading term, degree.
(b) Long run behavior: leading term
(c) Short run behavior: zeros and factoring
(d) Formula <-> graph
7. Rational functions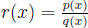 
where p(x), q(x) are polynomials
(a) Long run behavior: divide leading terms of p(x) and q(x).
(b) Short run behavior: find zeros of p(x), q(x) by factoring. They correspond
to zeros, vertical asymptotes, and holes for r(x).
(c) Formula <-> graph
8. Dominance: f(x) > g(x) when x is large
(a) Exponential functions: compare growth factor
(b) Power functions: compare power
(c) Increasing functions: exponential dominates power dominates logarithmic
(d) Decreasing functions: power dominates exponential, i.e. power functions
decrease slower.