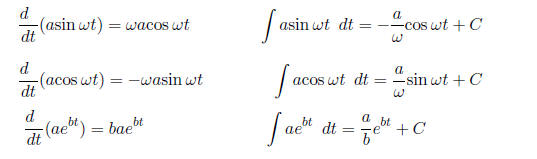Math Review
1 Geometry
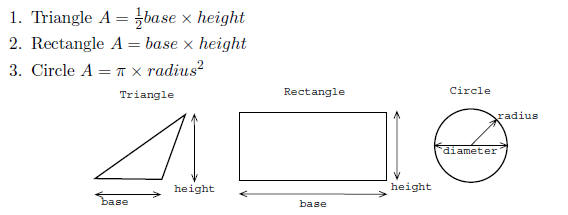
• Here are some areas of standard geometric figures that you should remember:
• The volume of a sphere is (4/3)πR3, its surface area is 4πR2.
• The circumference of a circle is 2πR, where R is the radius, or πD, where D
is the diameter
(D = 2R).
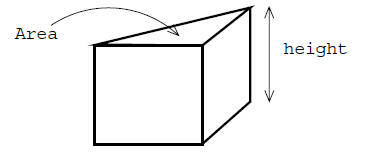
• The volume of a right figure is is V = A × h, where h is the height of the
figure, and A is
the area of the base. If the base is a circle, then we’re talking about a right
cylinder and
A = πR2. If the base is a rectangle, you get the idea.
2 Algebra
• Solving linear equations is easy: Ax + B = C implies the solution for x is
x = (C − B)/A.
Solving quadratic equations: Ax2 + Bx + C = 0 implies
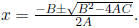
• Solving a system of 2 equations with 2 unknowns: if
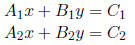
(where the Ai's, etc., are constants) then you can “solve” the first equation
for x like x =
(C1 − B1y)/A1 and insert this expression into the second equation. Then you will
have a
solution for y. Once you know y, you can use this value for y to solve for x.
3 Trigonometry
• In the figure, the trigonometric functions sine, cosine, and tangent acting
on the angle θ are
defined as follows
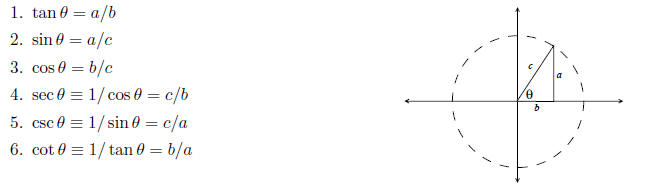
• A consequence of Pythagoras’ theorem is that sin2θ + cos2θ
= 1
• These are some useful values of the trig functions you should remember I
reminded you of,
but I will generally put these on exams for you:
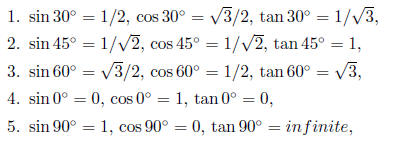
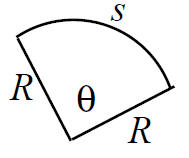
• Radian vs. Degree Measure of Angles: In the figure above, if c = 1, then
the circle drawn is
called the unit circle. The relationship between the length s of a piece of arc
and the radius
R and angle of arc θ is s = Rθ. When this relation is applied to the unit
circle, we see that
the angle θ=1 revolution has to be measured in a very particular way: in
“radians”. One
revolution = 360◦ = 2π “radians”.
1. 0◦ = 0 radians
2. 45◦ = π/4 radians
3. 90◦ = π/2 radians
4. 180◦ = π radians
5. 270◦ = 3π/2 radians
6. 360◦ = 2π radians
• You should convince yourself that you understand the graphs below. I don’t
expect you to to
memorize them, but they should make sense if you look at the particular values
of the sines
and cosines listed above (when degrees are converted to radians).

4 Calculus
• A function maps each possible value of an independent variable t to a value
of the dependent
variable x. We write x = f(t), or equivalently x = x(t).
• The derivative of the function x(t) at time t is defined by
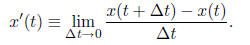
A common notation for “the derivative of x(t) with respect to t” is dx/dt .
The derivative dx/dt
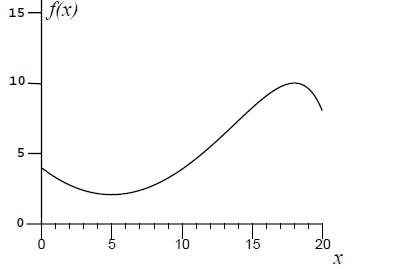
gives the slope of x(t). For example, the derivative of the function f(x) shown
in the figure
below is zero at x = 5 and x = 18. The derivative is positive between these two
points and
negative outside these two points.
• An antiderivative of f(t) is a function F(t) such that F'(t) = dF/dt = f(t).
Any antiderivative
plus a constant C is also an antiderivative, since the derivative of a constant
is zero. A
common notation for all the antiderivatives of f(t) is
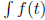 ,
which is called the indefinite
,
which is called the indefinite
integral.
• The definite integral of a function f(t) from t1 to t2 is
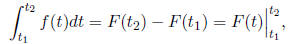
where F(t) is an antiderivative of f(t). The definite integral gives the area
under the function
between the limits of integration (t1 and t2).
• For a function of the form x(t) = atn:
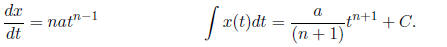
• For some common functions: