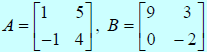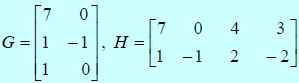Operations with Matrices
Lecture 4.5
Two matrices are said to be equal if they have the same
size and their corresponding
elements are equal. For example,
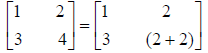
If all the elements are not equal then the matrices are not equal.
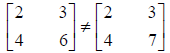
A zero matrix is a matrix in which all elements are zero.
The zero matrix is commonly
denoted O.
Two matrices A and B of the same size can be added or subtracted to produce a
matrix of
the same size. This is done by adding or subtracting the corresponding elements
in the two
matrices. For example,
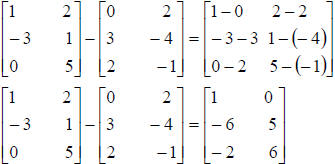
The additive commutative property, additive associate
property, and the additive identity
property all hold for matrix addition. Accordingly,
A + B = B + A
(A + B) + C = A + (B + C)
A + O = O + A = A
A matrix A may be multiplied by a real number called a scalar in the context of
matrix
algebra. The scalar product, denoted by cA, is a matrix obtained by multiplying
each entry of A
by c. For example,
If
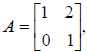
Then
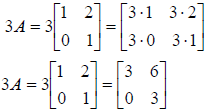
With certain restrictions, one matrix may be multiplied by
another matrix. The following
problem will help define matrix multiplication.
On a certain day Maria's Optical sold 32 frames, 30 poly-carbonate lenses, and 2
no-line bifocal lenses. If the prices for these goods on that day were $50 for
frames, $65 for poly-carbonate lenses, and $45 for no-line bifocal lenses, find
the
total revenue for Maria's Optical for that day. The day's sale of goods may be
represented by a matrix:
A = [32 30 2].
The sale prices for that day may be represented by another matrix:
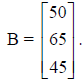
The first element in matrix A gives the number of frames
sold and the first
element in matrix B gives the selling price for each frame. Their product
32 · 50 yields the revenue from sold fames for the day. A similar interpretation
of
the second and third elements in the two matrices suggests that multiplying the
corresponding elements will obtain the respective revenues gained from the sale
of each product. Adding each of these sub-products would yield the total revenue
obtained from the sale of goods that day. Thus, multiplying the elements of
matrix
A by the corresponding element in matrix B and adding the products yields a
single number result representing the total revenue of the shop:
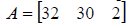
The shop made $3,640 from the sale of goods.
The above problem exemplifies a matrix product. In matrix multiplication each
element
of the matrix product is the sum of the products of the corresponding row from
the first matrix
and the corresponding column in the second matrix.
In general terms, if A is a matrix of dimension m× n and B is a matrix of
dimension
n × p (the number of columns of A equal the number of rows of B), then the
matrix product of A
and B, AB, is defined and is a matrix of dimension m× p . Schematically,
| Size of A | Size of B | ||
 |
|||
| Size of AB | |||
In less general terms, the following example will
illustrate the mechanics of matrix
multiplication.
If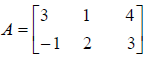
and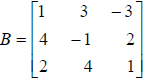 
Compute AB.
The dimension of matrix A is 2× 3, and the dimension of
matrix B is 3× 3. Since the
number of columns of matrix A is equal to the number of rows of matrix B, the
matrix product,
AB, is defined. (Note that the matrix product BA is not defined since the number
of columns in
matrix B does not equal the number of rows in matrix A. This phenomenon shows
that the
commutative property does not hold for matrix multiplication.) Furthermore, the
dimension of
matrix AB is 2× 3. Thus,
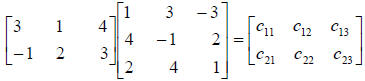
To determine the element c11, multiply the elements of Row
1 of A by the corresponding
elements of Column 1 of B and add the products. The position of each element
indicates the
procedure that obtains it. The element c11 occupies the first row and first
column of the matrix
product. Thus, it is obtained by multiplying the elements of the first row of A
by the
corresponding elements of the first column of B and adding the products.
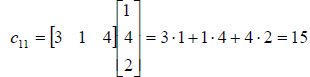
Similarly, element c12 is occupies the position of the
first row second column in the matrix
product. Therefore, it is obtained by multiplying the elements of the first row
of A by the
corresponding elements of the second column of B and adding the products.
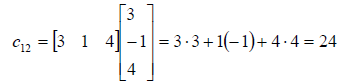
The remaining elements are found accordingly.
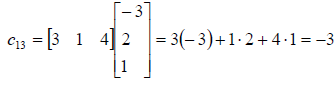
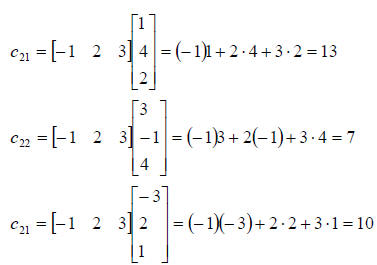
Thus, the matrix product AB is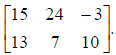
As mentioned above, in general, AB ≠ BA for matrices A and
B, so the commutative
property does not hold for matrix multiplication. However, the associative and
distributive
properties are valid. So, (AB)C = A(BC) and A(B+C) = AB + AC.
The square matrix of dimension n × n having "1s" along the main diagonal and
zeros
elsewhere is called the identity matrix of dimension n × n . In other words, a
row-reduced square
matrix is the identity matrix for that size square matrix. The identity matrix
of dimension 3× 3 is
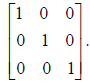
The identity matrix has the property that
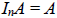for any n × r matrix A, and
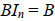for any
s × n matrix B. In particular, if A is a square matrix of dimension n × n , then
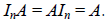
Example Exercises 4.5
Instruction: Operations with Matrices
Example 1
Scalar Multiplication
Consider matrix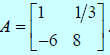
Find 6A. |
Multiply each element of A by six.
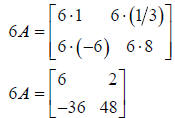
Example 2
Adding Matrices
| Consider the two matrices below.
What is the sum of A and B? What is the difference of A and B? |
The sum of two matrices is the matrix whose elements are
sums of the corresponding elements in
the addends.
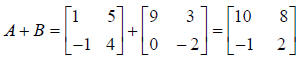
The difference of two matrices is the sum of the minuend
and the product of –1 and the
subtrahend.
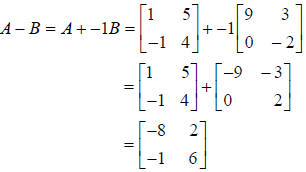
Example 3
Multiplying Matrices
| Consider the two matrices below.
What is the product GH? |
If GH is defined, then H must have as many rows as G has
columns. The product will have as
many rows as G and as many columns as H. Since G is a 3×2 and H is a 2×4, the
product GH is
defined as a 3×4 matrix.
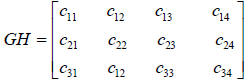
The element c11 is the sum of the
products of the elements in row one of G and column one in H;
the element c12 is the sum of the products of the elements in
row one of G and column two in H;
etc. Find the elements.
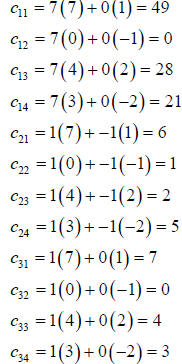
Write the product.
Practice Set 4.5
Perform the indicated operations.
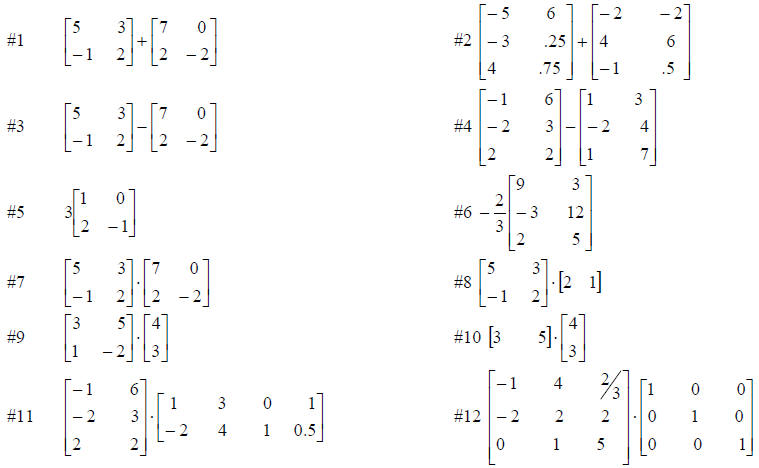
#13 Show with one example that multiplication of matrices
is not commutative.
#14 If the two matrices A and B below are equal, then solve for x, y, z, & w.
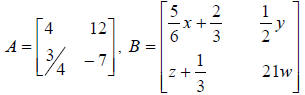
ANSWERS
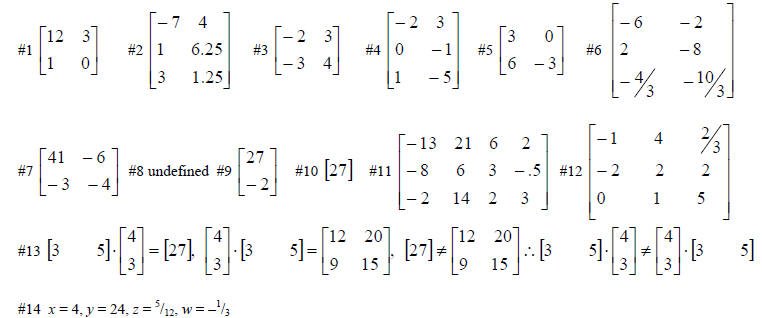
Study Exercise 4.5
Problems
For the problems below refer to the following matrices.
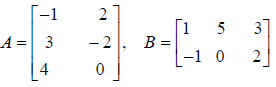
#1 Compute 3B
#2 Compute A + A
#3 Compute B · A.
#4 Compute A· B.