Worksheet on Rational Functions
A rational function is the quotient of two polynomial
functions, where the denominator is
not zero: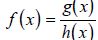 
I. The vertical asymptotes are lines which the
graph of the function approaches,
but never touches. They can be found by setting the denominator equal to zero
and solving for x. (See III for exceptions to this procedure.) If the
denominator
cannot equal zero, then there are no vertical asymptotes. The equations of the
vertical asymptotes will always be of the form x = a. The domain will consist of
all real numbers except those numbers which make the denominator equal zero.
Example: If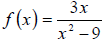 
, then the vertical asymptotes
are x = 3
and x = -3. The domain is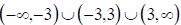 
.
1. Find the equations of the vertical asymptotes and the domains of each of
the following functions.
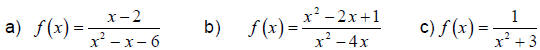
II. The horizontal asymptote is a line which the
graph of the function approaches, but
never touches as x gets very large or very small, i.e., as
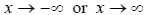. The
graph may cross the horizontal asymptote for some real value of x. The equation
of
the horizontal asymptote will always be of the form y = b. Since we are
examining
the function as x gets large without bound, the terms of greatest importance are
those with the largest exponent in both the numerator and denominator. There are
three cases to be considered.
A. If the degree of the numerator is less than the degree of the
denominator, then the horizontal asymptote is y = 0.
Example: 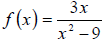. Consider the equation
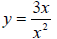(found by
considering only the highest degree term in numerator and
denominator). It reduces to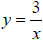 
. As x gets
large without
bound, the fraction gets smaller and smaller and approaches
0. Thus the equation of the asymptote is y = 0.
B. If the degree of the numerator equals the degree of
the denominator,
then the horizontal asymptote is y = the quotient of the coefficients of the
highest degree terms.
Example: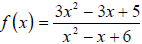 
. Consider the equation
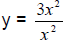. Since the
x2 terms will cancel, the horizontal asymptote is y = 3.
C. If the degree of the numerator is greater than the degree of the denominator,
then there is no horizontal asymptote, but there is an oblique asymptote.
(See IV).
III. The range can frequently be found by using the horizontal asymptote,
coupled with
the graph. It will be essential to see if the graph crosses the horizontal
asymptote.
A. Referring to the function in IIA, we found the horizontal asymptote to be
y = 0. Can f(x) ever equal 0? If f(x)=0, then the numerator must = 0.
3x = 0=> x = 0 . Therefore, the graph of f(x) crosses its own horizontal
asymptote at (0, 0). Looking at the graph of f(x) on the calculator shows
that the range in this case is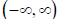 
.
B. Referring to the function in IIB, we found the horizontal asymptote to be
y = 3. Can f(x) ever equal 3? If 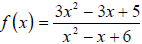is to equal
3, then we
see that 3x2 - 3x +18 = 3x2 - 3x + 5 . This implies that 18 = 5, which is
impossible. Therefore, the graph of f(x) does not cross the horizontal
asymptote in this case. Looking at the graph on the calculator and using
MINIMUM show that the range is [.74, 3), where the .74 is an
approximation.
2. Find the equation of the horizontal asymptote, the coordinates of the point
where
the graph crosses the horizontal asymptote (if it exists), and the ranges of
each of
the following functions.
III. In some cases there is a “hole” in the graph. This
happens when there is a factor
which cancels out of the numerator and denominator.
Example: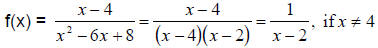
There will be a hole (but not an asymptote) at x=4. To
find the
corresponding y-value, substitute 4 in place of x in the reduced form of the
function. In this example, there is a hole at the point
.
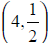3. Find the coordinates of the hole in the graph of
.
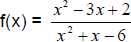IV. If the degree of the numerator is greater than the degree of the
denominator,
then there will be an oblique (or slant) asymptote instead of a horizontal
asymptote. To find the equation of the oblique asymptote, use long division as
follows. (could use synthetic division)
Example:
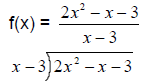Divide only the x into
the 2 x2 ; this gives 2x
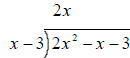Multiply the (x-3) by
the 2x
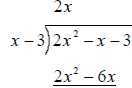Subtract and bring
down -3
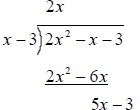Repeat above steps
until all terms are used
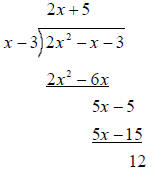
This means that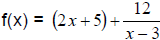 
. As x
gets large without bound, the fraction
will get smaller and smaller and approach zero. Therefore, the equation of the
oblique asymptote is y = 2x+5. There are no horizontal asymptote if there is an
oblique asymptote.
4. Find the equation of the oblique asymptote.
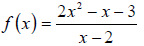
V. Find the y-intercept, let x=0. Some functions may not have a y-intercept. No
function will ever have more than one y-intercept, since this would cause it tot
fail the
vertical line test for a function.
Example: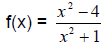 
. If x=0, then y = -4, so the
y-intercept is (0,-4).
5. Find the y-intercept of each of the following functions.
VI. To find the x-intercept, let y = 0. The only way a fraction can equal zero
is if its
numerator equals 0, but its denominator does not. A function may have 0, 1, or
more x-intercepts.
Example: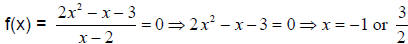 
. Make sure that
neither of these values causes the denominator to = 0. The x-intercepts are (-1,
0),
and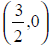 
.
6. Find the x-intercepts of each of the following functions.
