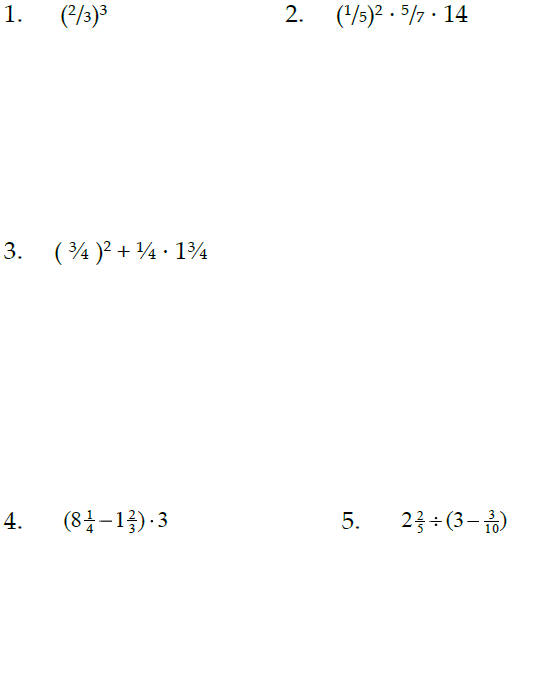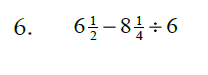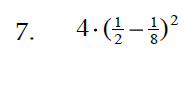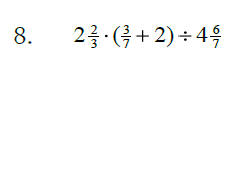Fractions and Mixed Numbers
Sec. 3.1 Least Common Multiple
The least common multiple (LCM) of two (or 3) numbers is the smallest
number that the 2 (or 3) numbers will divide into. The LCM is used for the least
common denominator which is needed in addition and subtraction of fractions.
Example: Find the LCM of 12 and 18, using prime factorization.
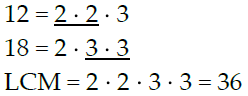
Find the LCM, using prime factorization:
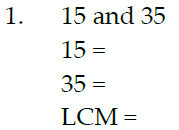
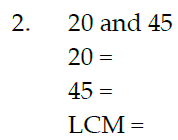
3. 21 and 70
21 =
70 =
LCM =
4. 90 and 105
90 =
105 =
LCM =
5. 15, 21 and 35
15 =
21 =
35 =
LCM =
6. 8, 20 and 60
8 =
20 =
60 =
LCM =
Use prime factorization to find the LCM of…
7. 14 and 35
14 =
35 =
LCM =
8. 21 and 28
21 =
28 =
LCM =
9. 50 and 75
50 =
75 =
LCM =
10. 63 and 90
63 =
90 =
LCM =
11. 15, 27 and 18
15 =
27 =
18 =
LCM =
Sec. 3.2 & 3.3 Adding and Subtracting Fractions
A common denominator is needed for adding and
subtracting fractions – it's the LCM!
Add or Subtract, leaving your answer as a reduced fraction:


Solve:
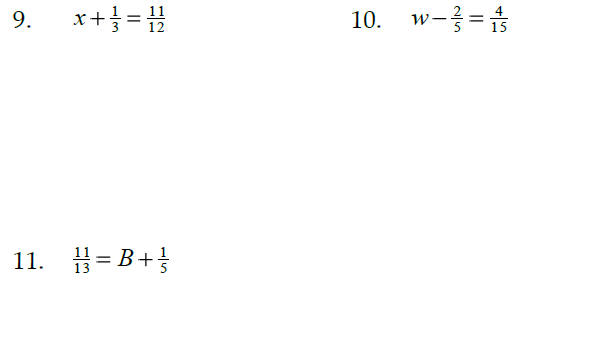
12. John walked 1/2 mile to the student union and then 1/3 mile to class. How far did John walk?
13. Sally bought 1/4 lb. of peanut butter fudge and 3/8
lb. of
rocky road fudge. How much fudge did she buy?
14. Judy has 3/4 lb. of a candy corn and peanut mixture.
If
this contains 1/3 lb. peanuts, how many pounds of candy
corn are in the mix?
3.4 & 3.5 Adding and Subtracting Mixed Numbers
Common denominators are needed to add and subtract
mixed numbers, but it is not necessary to change them into
improper fractions. Subtraction may require borrowing.
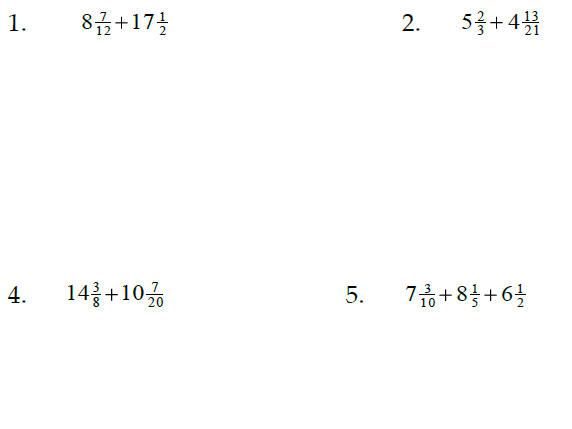
6. Compare 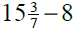 and
and
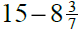
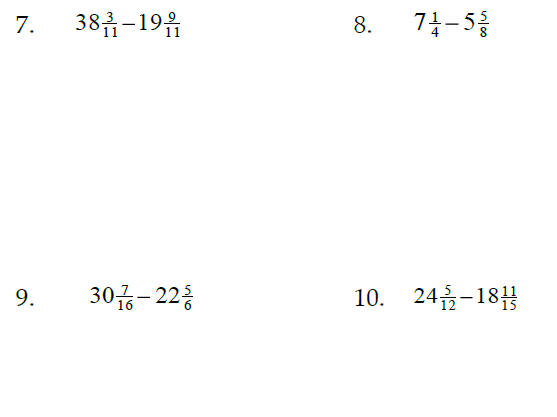
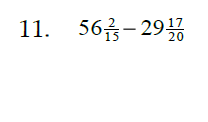
Sec. 3.6 Multiplying & Dividing Mixed Numbers
Ideas to remember:
* No common denominator is needed.
* Mixed numbers must be changed into improper
fractions.
* When multiplying, try to reduce first by cancelling.
* When dividing, the rule is “invert and multiply.”
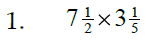
Steps:
* Convert mixed #s to
improper fractions
* Try to cancel
* Multiply across
* Check for reducing
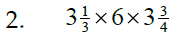
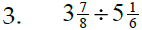
Steps:
* Convert mixed #s to
improper fractions
* Invert (flip over) 2nd fraction
* Use steps for multiplying
…try to cancel
…multiply across
…check for reducing
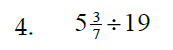
An Assortment of Word Problems for Chapter 3:
1. Jimmy poured 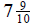 yards of cement for a
fountain.
yards of cement for a
fountain.
Another fountain took 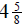 yards. How much cement
yards. How much cement
was used for both fountains?
2. Tammy has a piece of rope that measures 210 inches.
How many pieces of rope 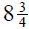 inches long can she
cut
inches long can she
cut
from the original piece?
3. Larry works a maximum of 18 hours per week at his
work-study job at the college he attends. If he works
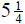 hours one day,
hours one day,
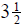 hours the next day and
hours the next day and
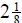 hours
hours
the third day, how many more hours must be work to
complete his 18 hours?
4. A stock has a value of
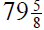 on Monday. On Tuesday it
on Monday. On Tuesday it
goes up 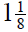 , and on Wednesday it goes down
, and on Wednesday it goes down
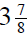 .
.
What is the new value?
5. The framework of a wall is
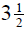 in. thick. We apply
in. thick. We apply
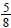 -in.
-in.
wall board and 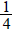 -in. paneling to the inside.
Siding
-in. paneling to the inside.
Siding
that is 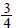 in. thick is applied to the outside.
What is the
in. thick is applied to the outside.
What is the
finished thickness of the wall?
6. If you cut 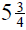 yd and
yd and
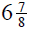 yd lengths from a 20-yd roll of
yd lengths from a 20-yd roll of
wallpaper, how much paper remains on the roll?
Sec. 3.7 Order of Operations with Fractions
Perform the indicated operations in the correct order: