Paris Math Problem Set: Week 1

1 Logistic map

Discuss the behavior of the Logistic map for a > 4.

2 Periodic orbits of the tent map

The tent map is defined on the interval [0, 1] by

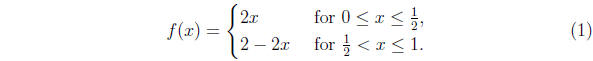
Find all the periodic orbits of this map, and determine their stability
(i.e. the rate at which perturbations to the orbit deviate from the orbit, per
iterate). What is the value of the Lyapunov exponent for chaotic orbits of
this map?

3 Exploration of cubic chaos

Discuss the behavior of the iterated map

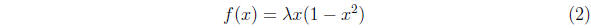
using any combination of numerical simulations and mathematical analyses
you can bring to bear on the problem. This is a fairly open-ended problem,
and determining the right questions to ask in analyzing such a system is a
major part of what I am looking for in the solution.

4

(a) Let z = x + iy, where x and y are real, and let F(z) be the function
which takes z to the complex number x² − iy². Show that F is not analytic
(complex-differentiable). Let G(z) be a non-constant function whose range
is the real axis. Can G be analytic?

(b) Find the image of the unit circle in the complex plane, under the first
and second iterates of the map z² − 1. Sketch your result. You may wish to
write a Python script to plot the answer.

5 Designing Python objects

Design an object to find a root of f(x) = 0 in the interval [a, b], for an
arbitrary continuous function f, using the bisection method. The input
interval satisfies the property f(a)f(b) < 0. The general idea of the bisection
method is as follows: You consider the two sub-intevals [a, (a + b)/2] and
[(a + b)/2, b]. Using the fact that f is continuous, you can determine which
of the two intervals contains a root. By iterating the process, you can achieve
the accuracy you desire.

Add an additional method to the object which finds a root using Newton’s
method, starting from a specified initial guess. For this method, you
may require that the user supply a function fprime(x) which returns the
derivative of f.

Test your object on a few functions you have made up.

6 Overloading operators

Define a ”fraction” object, which stores a general rational number a/b where
a and b are integers. Overload all the usual arithmetic operators (addition,
subtraction, multiplication, division). Make sure to allow for arithmetic with
regular integers, as well as arithmetic with other fraction objects. Also define
the method so that the fraction prints out in some nice way.

Note that after performing arithmetic on fractions, your fraction will not
generally be in reduced form. That is, the numerator and denominator will
often have common factors that should be divided out. The following little
function uses Euclid’s algorithm to find the greatest common divisor of two
integers. You can make use of it in your object to put your fractions in
reduced form.



Create a few fractions, and try out arithmetic with them to make sure
everything is working properly

Now use your object to write a function which computes the rational
number given by the first n terms in the Taylor series for e, the base of the
natural logarithms. Show some results for a range of n. Check your results
by converting the numerator and denominator into floats and dividing (e.g.
float(a)/float(b)), comparing the result to the correct double-precision
value of e given by math.e. Note that for rather moderate values of n, your
rational number will beat the maximum precision of Python floating point
numbers. In essence, you have written a system for doing arbitrary precision
rational arithmetic.