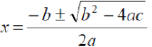Math 111 Chapter 1 Sections 1 & 2 Reviews
| Mixtures : (1st % × Amt) + (2nd % × Amt) = Final % × Amt
How many gallons of cream containing 25% butter fat
and milk Let x = # gal cream 0.25x = # gal of butter fat in cream 0.25x + 0.035(50 - x) = 0.125(50) x = 20.93 (rounded) |
| Your 8 quart radiator is full with a 30%
antifreeze mixture. How much pure antifreeze should be added to get a 50% antifreeze mixture. |
| In the chemistry lab you have 20 oz of a 10% acid solution. How much 60% acid solution should you add to get a 35% acid solution? |
| Work Problems: (part done by A ) + (part done by B) = 1 whole job
Ron, Mike, and Tim are going to paint a house
together. Ron can Let t be time needed to paint the side. (1/4)t + (1/3)t + (1/2)t = 1 |
Section 1.2 Quadratic Equations and Their
Applications Solve by factoring Solve by factoring Solve by taking the square root Solve by taking the square root Solve by completing the square Solve by completing the square Solve by using the Quadratic Formula Solve by using the Quadratic Formula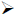 The discriminant of a Quadratic Equations The discriminant of a Quadratic EquationsApplications |
| A quadratic equation is an equation that can be
written in the following standard form: ax² + bx + c = 0, where a,b,c are real numbers and a ≠ 0 The Zero Product Principle If A and B are algebraic expressions such that AB = 0, then A = 0 or B = 0 |
| 1.2: Factoring and using Zero Product Principle Solve by factoring... x2 + x = 12 Solve by
factoring... 2x2 - 5x
= 12 |
| 1.2: Square Root Procedure If x2 = c, then 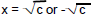 Solve by using the square root method. 2x2 = 48
Solve by using the square root method. (x + 2)2 = 36 |
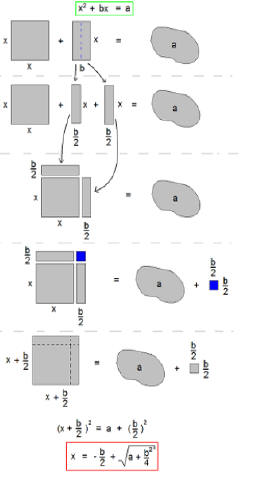
| Geometrically Completing the Square
|
| 1.2: Completing the Square
Solve by completing the square
|
| 1.2: Completing the Square Solve by "completing the square" x2 - 2x- 5 = 10 2 x2 + 4x - 4= 0 |
| The Quadratic Formula
The solutions of the equation
a ≠ 0 Solve by using the quadratic equation : 12x2 - x - 6 = 0 x2 = 2x - 2 |
| 1.2: Discriminant and solutions to the quadratic
equation The equation ax2 + bx + c = 0 , with real coefficients and a≠0, has as its discriminant b2 - 4ac If b2 - 4ac > 0 then two distinct real solutions. If b2 - 4ac = 0 then one real solution. If b2 - 4ac < 0 then two distinct nonreal complex solutions. The solutions are conjugates of each other |
| Determine discriminant and state the number of
solutions a) 4x2 - 5x + 3 = 0 b) x2 + 2x - 15 = 0 c) 4x2 + 12x + 9 = 0 Now graphically |
| 1.2: Applications The
Pythagorean Theorem a2 + b2 = c2 Garfield's Proof of the Pythagorean Theorem |



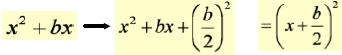
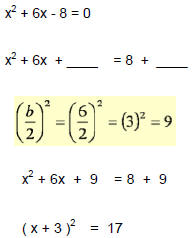
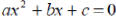 are :
are :