Vectors

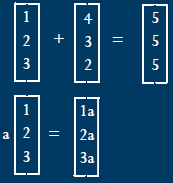	Vectors
	Vectors * Scalars
v=Q-P	Vector from P to Q

Example Vectors

Geometric Vectors
Directed Line Segments
Scalar-Vector Multiplication
Changes Length
Maintains Direction
Vector-Vector Addition
Head-to-Tail Axiom

Euclidean Spaces

Inner (dot) product
u·v=v·u
(au+bv)·w=au·w+bv·w
v·v>0(v!=0)
0·0=0
if u·v=0, then u and v orthogonal
|v|=sqrt(v·v)
Add concepts of affine spaces, such as points
P-Q is a vector
|P-Q|=sqrt((P-Q)·(P-Q))
Angle between two vectors
u·v=|u||v|cos(theta)
Equation for a circle
|Q-P|=r
sqrt((Q-P)·(Q-P))=r
(Q-P)·(Q-P)=r²

Dot Product

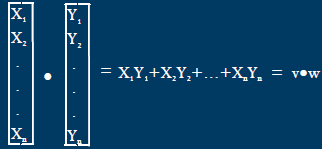
v·w = w·v v·v==0 only when v==0

||v|| = sqrt(v·v) = Distance to v from origin

||v-w|| = Distance from v to w

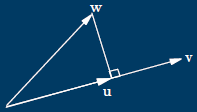
Projections

Finding the shortest distance between a
point to a line or plane
Start with two vectors
Divide one into two parts
One parallel, one orthogonal to the second
original vector
v is first vector, w is second vector

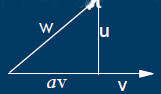
w=av+u
Parallel part, v
Orthogonal part, u
u·v=0
w·v=av·v+u·v=av·v
a=-(w·v)/(v·v)
av is projection of w onto v
u=w-[(w·v)/(v·v)]v

Normalized Vectors

Length of One
Unit vector
v'=v/||v||

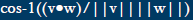
Angle Between v and w
Calulating the length of a rotated vector. The dot product
of v and w is the length of the projection of w onto v,
provided v is a unit vector
||u|| =||w||cos(theta)
=||w||((v·w)/||v||||w||)

OpenGL and Affine Spaces

Positions always defined relative to the
origin of the current coordinate system
Transform the coordinate system to take
positions relative to some other point
Necessary for computing distances, angles,
etc.

Matrices

nxm array of scalars
n Rows
m Columns
If m=n then square matrix
The elements of a matrix A are {a_ij}, i=1,...,n,
j=1,...,n
A=[a_ij]
Transpose of A of n is mxn matrix with rows
and columns interchanged
A^T=[a_ji]
Single row or single column
Row Matrix
Column Matrix
b=[b_i]
Transpose of a row matrix is a column
matrix
Transpose of a column matrix is a row
matrix

Identity Matrix MI=M

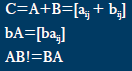
Identity Matrix

1's along diagonal
I=[a_ij] a_ij={1 if i=j, 0 otherwise
AI=A
IB=B

Matrix Operations

Scalar-matrix multiplication
aA=[aa_ij]
a(bA)=(ab)A
abA=baA
Matrix-matrix addition
C=A+B=[a_ij+b_ij]
Commutative
Associative
Matrix-matrix multiplication
Product of nxl and lxm is nxm
Middle dimmension MUST match
C=AB=[c_ij]
c_ij=Sum[k=1,l]a_ikb_kj
Associative
NOT Commutative
AB!=BA
May in fact not even be defined
Order matters
Application to Transformations

Row and Column Matrices

Representation of vectors or points
p=[x y z]^T
p^T=[x y z]
Transformation - Square matrix
Point - Column matrix of 2, 3, or 4 pts.
p'=Ap
Transforms p by A
p'=ABCp
Concatenations of transformations
(AB)^T=B^TA^T