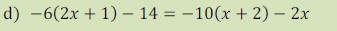Solving Linear Equations
Review Addition and Multiplication properties of equality
Core Concepts:
| Strategy for solving linear equations with one variable: 1. Simplify both sides of the equation •Get rid of fractions or decimals •Clear Parentheses (Use distributive property as needed) •Combine like terms on each side of equation 2. Use addition property of equality to get all variable terms on one side and constants on the other (Keep using this property as many times as needed). 3. Use multiplication property to make the coefficient of the variable = one 4. Check your solution in original equation |
->We have done lots of problems using this strategy so
far, we are just making it more formal.
•Remember to use distributive property on a negative grouping, multiply all
inside by -1
•EX: 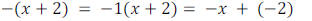
and 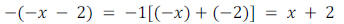
Solve variety of problems:
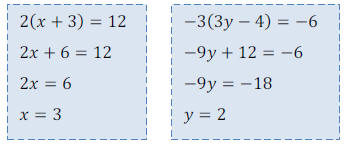
->What happens when we have fractions or decimals in the
problems? Well, we can deal with
them as we normally would, or we can use a trick to get rid of them. Here it is:
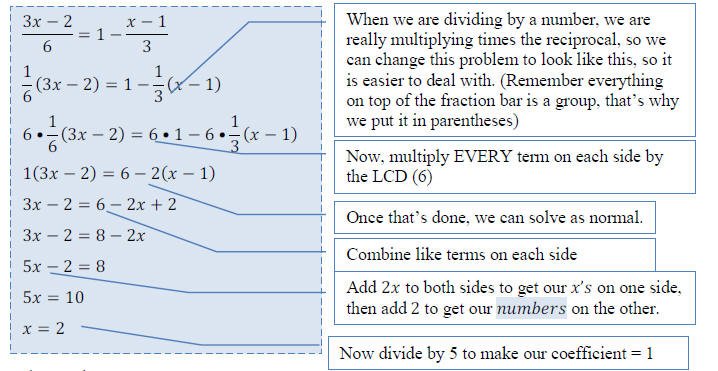
| •Clear fractions or decimals by multiplying both
sides by a common denominator (for fractions) or a power of 10 (for decimals) |
->Here’s how it works: Fractions
•All you have to do is look at the problem and determine the LCD of all the
fractions from
BOTH sides, then multiply both sides of the equations by the LCD (remember we
can
multiply both sides of an equation by the same number and we haven’t changed the
equation – mult property of equality)
•This will magically make all the fractions disappear!
•EX: Here is an example where we would have to find the LCD for at least two of
these
fractions anyway, so why not just use it early to clear the fractions.
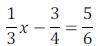
Instead of trying to add the fractions, I’m going to get rid of them – watch!

• You try one: 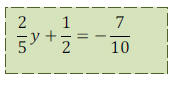
•Of course you don’t HAVE to clear the fractions, you can
just add or subtract them as
normal. It’s up to you. There are times when I wouldn’t want to clear the
fractions
because it doesn’t really matter.
•Look at this: 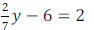 This
problem has only one fraction in it, and if I look at it, I
This
problem has only one fraction in it, and if I look at it, I
can see that I am never going to have to add the fraction to anything (there are
no other
variable terms in the equation). So I can just move my constants together (since
they’re
not fractions) by using the addition property of equality.
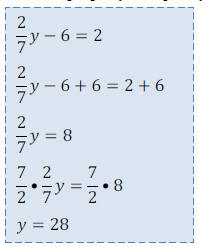
->What about Decimals?
•We don’t need an LCD for decimals, what we need is a
power of 10 because for every 10
we multiply times a decimal, the decimal point moves one to the right. We just
need to
figure out how many places we have to move the decimal and that tells us which
power
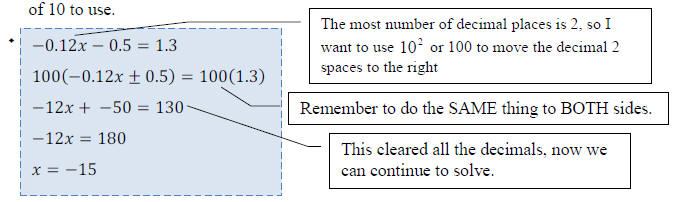
NOTE: We didn’t change the problem because we did the
same thing to both sides. There is no
need to worry about the decimal point once it is gone!
•Now you do one:
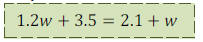
->Let’s do some more complicated ones to show you what can happen
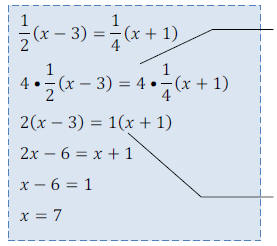 |
The LCD of both sides is 4. Remember
you are multiplying each term on both sides by 4, but in this case, we haven’t distributed yet, so we just need to multiply the numbers outside the parentheses by 4. It will get multiplied by the stuff inside once we distribute. OR you can distribute first then multiply by the LCD. |
| Once fractions are cleared, you can continue to solve |
•NOTE: we have to be VERY CAREFUL here. Remember we are
multiplying each
TERM by the LCD. How many terms are on the left side at the beginning? Only one,
because a term is stuff multiplied together and we have ½ multiplied by blob
(the stuff in
parentheses). So, when we multiply by the LCD, we only need to multiply by the
thing
on the outside of the parentheses because that will eventually get multiplied
into the
•parentheses when we distribute (the associative property).
We could have distributed first, then multiplied each term by the LCD (4) and we
would
get the same answer. Whichever way you want to do it is fine.
•Sometimes it can look more complicated, but it’s basically the same type of
problem.
• EX:
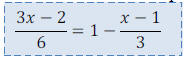
•Classwork:
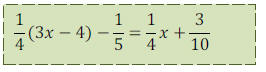
->Weird stuff that can sometimes happen with equations:
•Sometimes equations can have no solution. We can tell if there are no
solutions, if we
end up with a contradictory statement when we are solving. Example:
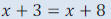 If we subtract
x from both sides, we get: If we subtract
x from both sides, we get: 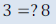 This is a contradiction which means
we have This is a contradiction which means
we haveNO Solution or the Null set which is this symbol: 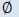 |
•Other times the x might go away, and we have a true statement, but the x is gone:
 If we subtract
x from both sides, we get: If we subtract
x from both sides, we get: 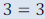 This statement is true, but we have
no x left. This statement is true, but we have
no x left.This means that ANY Real number will work in this equation. So the solution set is ALL REAL NUMBERS. This kind of equation is called an identity. |
•The above examples are fairly obvious, but sometimes it
isn’t easy to see. We can only
find out after we simplify both sides.
•EX:
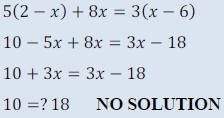
->Mixed Classwork:
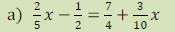
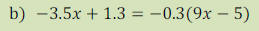
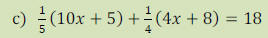 HINT: Distribute first
here
HINT: Distribute first
here