Composition of Functions
Part 1: An Example
1. There are 3 scales used in measuring temperature –
Fahrenheit, Celsius and Kelvin. One can
convert Fahrenheit reading to Celsius using 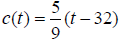 ,
where t represents temperature
,
where t represents temperature
in degrees Fahrenheit. Likewise, Celsius readings can be converted to Kelvin
using
k(t) = t + 273 , where t represents temperature in degrees Celsius.
a. I want to convert 100° F to the Kelvin scale. Make the
conversion and explain your
process.
b. Convert − 5 ° F to Kelvin
c. Convert 115° F to Kelvin
d. Generalize this process by creating a function that
will take measurements in degrees
Fahrenheit and convert them into degrees Kelvin, and explain how you did that.
Model #1
Function Chains
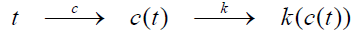
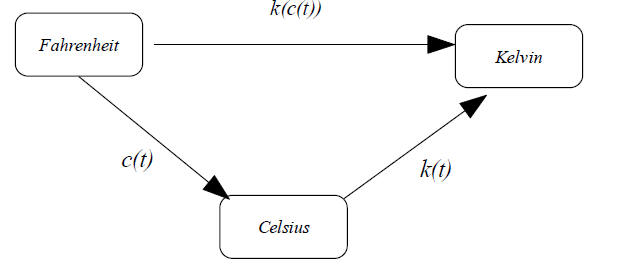
Model #2
Change of Variable
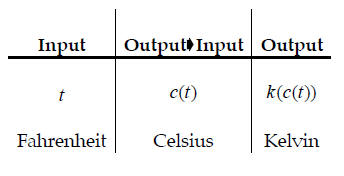
Model #3
Modified T-table
Model #4?
Part 2: Some Big Ideas about Function Composition
1. In mathematics, combining simple functions with
"composition" to form more complicated
functions is somewhat similar to the way that in chemistry elements can be
combined
through chemical bonds to form compounds.
2. Function composition combines a pair of functions f and
g into a single "composite"
function written f o g . The composite function operates in a chain where the
output of
function g is used as the input of function f.
3. Sometimes the order of the composition of two functions
makes a difference, while at other
times it doesn't. That is, for some functions f and g, f o g = g o f while for
other functions f
and g, f o g ≠ g o f
4. There are three common operations by which two
functions f and g can be combined to
form another function h: addition ( f + g) , multiplication ( f * g) , and
composition f o g .
The three are quite different, and function composition needs to be clearly
distinguished
from the other two.
5. Given a graph of a function f, graphs of f (x + 2) and
f (x) + 2 represent translations of this
graph, while graphs of f (2x) and 2 f (x) represent expansions or contractions
of this graph.
These transformations of graphs can be expressed in terms of the composition of
f.
6. Iteration (repeating a process over and over) can be
expressed in terms of the composition
of a function with itself.


