MATH 1090-4 EXAM 2 SOLUTIONS

1. (a) Find an equation of a line parallel to the line x = 4 and passing
through the point (15,−2).

x = 15

(b) Find an equation of a line perpendicular to the line x = 4 and
passing through the point (15,−2).

y = −2

2. Find an equation of a line perpendicular to the line y = −2x + 3 and
passing through the point (5, 1).

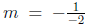(slopes of perpendicular lines are mutually opposite and
reciprocal)
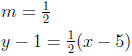  (point-slope equation of a line)


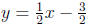
3. Find the intercepts and the vertex of the parabola y = 49 − (x − 3)²
and determine whether the vertex is a minimum or a maximum.

x-intercepts:

y = 0
49 − (x − 3)² = 0
49 = (x − 3)²
x − 3 = 7 or x − 3 = −7
x = 10 or x = −4
(10, 0) and (−4, 0)

y-intercept:

x = 0
y = 49 − (−3)²
y = 40
(0, 40)

Vertex is the point (3, 49) and it is a maximum since the leading coef-
ficient is negative.

4. The company will supply 50 units when the price of a product is $16
and 60 units when the price is $21. Find the supply function assuming
it is linear.

Since the supply function is linear, its graph is a line passing through
the points (50, 16) and (60, 21).

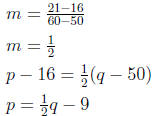
5. The demand function for a product is p = 12 − 2q where p is the price
in dollars when q units are demanded. Form the revenue function R,
determine the level of production that will maximize the revenue and
the maximum revenue.

Since revenue=price*quantity,

R = (12 − 2q)q
R = −2q² + 12q

The maximum is obtained when

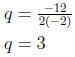
The maximum revenue is

R = (12 − 2 · 3) · 3
R = 18

6. Solve the system

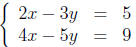
−4x + 6y = −10 (multiplying the first equation by -2)
y = −1 (adding the above to the second equation)
2x − 3(−1) = 5
2x = 2
x = 1

7. Nat invested $1000 at the rate 8% over 5 years compounded quarterly.
Find the compound amount at the end of 5 years.



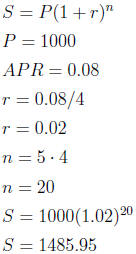
8. The population of a town of 20000 declines 1% annually. Find the
population after 10 years.

P = 20000(0.99)^t where P is the population after t years.
P = 20000(0.99)¹⁰
P = 18087.64

Approximately 18088.

9. Solve for x:

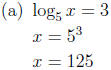
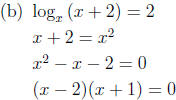
x = 2 (discard x = −1 because x is the base of a logarithm, hence
it cannot be negative)

10. Solve for x: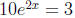

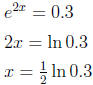
11. Let a = log x and b = log y. Rewrite 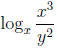in terms of a and b.

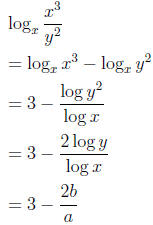
12. Solve for x:

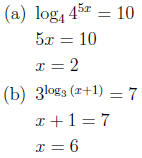
13. Solve for x: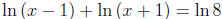



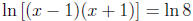
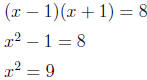
x = 3 (discard x = −3 since x − 1 and x + 1 must be positive)

14. Solve for x: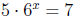

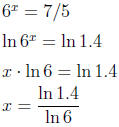
15. The number of milligrams N of a radioactive substance present after t
years is given by 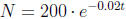. After how many years will there be
90 milligrams present?

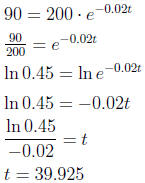
After approximately 40 years.