Arithmetic
Absolute Value | |
1. Simplify inside the absolute values first.
2. Whatever number is inside the absolute value becomes (or stays positive)
when you take the absolute value.
• Example:
|3 − 7| = | − 4| = 4
| − 3 + 7| = |4| = 4
Addition +
1. Identify the signs of the numbers that are to be added.
(a) For the same sign:
i. Add the numbers (ignoring the signs)
ii. Attach the common sign to your answer
(b) For different signs:
i. Ignoring the signs, identify the largest number.
ii. Subtract the numbers (ignoring the signs)
iii. Attach the sign of the number that you identified in step i.
• Example:
−4 + (−8) 
−4 and −8 have the same sign -
4 + 8 = 12 add the numbers
−4 + (−8) = −12 attach the sign identified earlier
• Example:
−4 + 8 −4 and 8 have the different signs
8 is larger than 4 so the answer will be positive
8 − 4 = 4 add the numbers
−4 + 8 = 4 attach the sign identified earlier
Subtraction -
1. Identify the two numbers being subtracted
2. Leave the first number alone and add the opposite of the second number
(If the second number was positive it should be negative. If it was negative
it should be positive.)
3. Follow the rules of addition.
• Example:
−4 − (−8) −4 and −8 are the numbers being subtracted
−4 + (+8) leave the first alone and add the opposite
−4 − (−8) = −4 + (+8) = 4
follow the rules for addition
• Example:
−4 − 8 −4 and 8 are the two numbers being subtracted
−4 + (−8) leave the first alone and add the opposite
−4 − 8 = −4 + (−8) = −12 follow the rules for addition
Multiplication ×, ( )( ), ·
1. Multiply the numbers (ignoring the signs)
2. The answer is positive if they have the same signs.
3. The answer is negative if they have different signs.
4. If you have more than 2 numbers, use the above but you must calculate
positive or negative with only two numbers at a time. Alternatively,
count the amount of negative numbers. If there are an even number of
negatives the answer is positive. If there are an odd number of negatives
the answer is negative.
• Example:
−4 × −8 −4 and − 8 are the two numbers being multiplied
4 × 8 = 32 multiply ignoring the signs
−4 × −8 = 32 same sign so positive
• Example:
−4 × 8 −4 and 8 are the two numbers being multiplied
4 × 8 = 32 multiply ignoring the signs
−4 × 8 = −32 different signs so negative
• Example:
−4 × 2 × −3 −4, 2 and 8 are the three numbers being multiplied
4 × 2 × 3 = 24 multiply ignoring the signs
−4 × 2 × −3 = 24 since there are two negative numbers,
−4 and − 3, and two is even the answer is positive.
Division ÷, /
1. Divide the numbers (ignoring the signs)
2. The answer is positive if they have the same signs.
3. The answer is negative if they have different signs.
4. If you have more than 2 numbers, use the above but you must calculate
positive or negative with only two numbers at a time. Alternatively,
count the amount of negative numbers. If there are an even number of
negatives the answer is positive. If there are an odd number of negatives
the answer is negative.
• Example:
−8 ÷ −4 −4 and −8 are the two numbers being divided
8 ÷ 4 = 2 divide ignoring the signs
−8 ÷ −4 = 2 same sign so positive
• Example:
−8 ÷ 4 4 and −8 are the two numbers being divided
8 ÷ 4 = 2 divide ignoring the signs
−8 ÷ 4 = −2 different sign so negative
NOTE: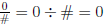 
and 
is undefined.
Dealing with Decimals
Be NEAT
1. Addition/Subtraction
(a) Follow the rules above for addition or subtraction being sure to line
up the decimals
• Example: 1.41 − 3.2 = 1.41 + (−3.2)
(add the opposite)
different signs subtract
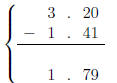
so 1.41 − 3.2 = −1.79 (since
3.2 > 1.41)
2. Multiplication
(a) Multiply the numbers together (ignoring signs and decimals)
(b) Count how many digits were to the right of the decimal (the total for
both numbers)
(c) Place the decimal so that the same number of digits is to the right of
the decimal in the answer
(d) Find the sign by the rules of multiplication above (same sign positive,
different signs negative)
• Example: (-.05)(.0026)=
Step (a)
| Step (b) |
−.05 has 2 digits to the right of the decimal .0026 has 4 digits to the right of the decimal |
 |
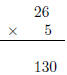| there is a total of 6 digits to the right of the decimal | ||
Step (c) & (d)
So, (−.05)(.0026) = −.000130 notice the 6 digits to the right of
the decimal including 130 with the zeros the left as place holders.
Also, the answer is negative since the signs are different.