Second Inter-term Math Exam

No books or notes. The percentage of each question is next to the question number. There are 5 extra points.

1. (8)
Determine the Hasse diagram of the relation on A= {1,2,3,4,5} whose matrix is shown.

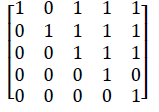
2. (4)
Determine if the statements are equivalent, justify your conclusion:
- If a є A is a maximal element, then there is no c є A such that a<c.
- If a є A is a maximal element, then for all b є A b≤a.

3. (9)
Determine the greatest and least elements if they exist of the poset A= {2,3,4,6,12,18,24,36} with the partial order of divisibility.

4. (6)
Define for any relation:
a) Symmetry

b) Transitivity

c) An equivalence relation

5. (6)
Describe the equivalence groups formed by the positive integers using the relation “same remainder on division by 5”. Prove whether or not these groups form a partition of the positive integers.

6. (8)
Define:
a) A function
b) An onto function
c) The inverse of a function
d) The composition of two functions

7. (6)
What must be true for the composition of two functions to have an inverse? Prove that these conditions are necessary

8. (8)
a. Draw a directed graph to represent the following matrix:

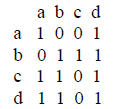
b. How do you find all the paths of length three in this graph?

9. (6)
Let L =P(S) be the lattice of all subsets of a set S under the relation of containment. Let T be a subset of S. Show that P(T) is a sublattice of L.

10. (4)
Is the poset A = {2,3,6,12,24,36,72} under the relation of divisibility a lattice?

11. (4)
Show that in a Boolean Algebra, for any a, b, and c ((aVc) ∧ (b’ V c))’ = (a’ V b) ∧ c’.

12. (8)
Show that (A, R) is a poset. Let A = {a,b,c,d,e,f,g,h} and R be the relation defined by

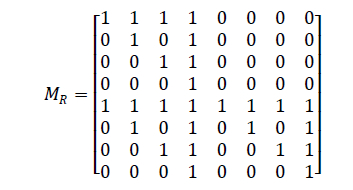
13. (4)
Show that in a Boolean algebra, the following statement is equivalent for any a and b.
a ∧ b = a

14. (4)
Consider all the two element subsets of the set {1, 2, 3, … , 150}. Show that if you add the elements of these two element subsets together at least two of them must have the same sum?

15. (6)
Given the graph below:

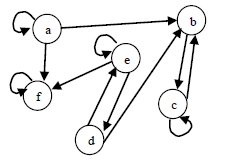
a) Describe this graph as a set of relations, R.

b) Describe this graph with a connectivity matrix.

16. (9)
a) Define the “transitive closure” of a set of relations.

b) Describe (carefully) the steps for how the connectivity matrix of a graph can be used to create the “transitive closure” of that graph. Use these steps on the graph of problem 15.