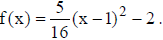Quadratic Functions

• A quadratic function has the form f (x) = ax² + b x + c where a, b, and c are real numbers
and a ≠ 0. The graph of a quadratic function is a parabola.

• The basic function f (x) = x² is a quadratic function. This parabola opens up with vertex at the
origin and axis of symmetry x = 0.

• In general, if a > 0, the parabola opens up; if a < 0, the parabola opens down.

• We will let ( h, k ) represent the vertex of a parabola. The standard form for a quadratic function is
f (x) = a (x − h)² + k . This form is useful since it incorporates the vertex.

• examples :
f (x) = 5x² + 3x −1 opens up since 5 > 0.

f (x) = −2x² + 6x +10 opens down since –2 < 0.

f (x) = 3(x − 2)² + 5 opens up (why?) and has vertex ( 2, 5 ).

• example : Let f (x) = −(x + 3)² − 4 .

Which way does this parabola open?

Give the vertex.

Find any x-intercepts.

Find the y-intercept.

Sketch the graph.

• If a quadratic function is not given in standard form, we can determine the vertex by using the
following result:

The vertex of f (x) = ax² + bx + c is at

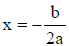
• example : Let f (x) = 3x² + 4x −1. Find the coordinates of the vertex.
The vertex is at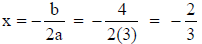

The y-coordinate of the vertex is f (−2 / 3) = 3(−2 / 3)² + 4(− 2 / 3)−1 = − 7 / 3

The vertex is at ( –2/3, –7/3).

• When a parabola opens up, the y-coordinate of the vertex (k) corresponds to the minimum value of
the function.

When a parabola opens down, the y-coordinate of the vertex corresponds to the maximum value of
the function.

• example : Let f (x) = 3x² + 4x −1. Since this parabola opens up, it has a minimum value of –7/3
which occurs at x = –2/3.

• Many application problems can be solved by finding the max or min of a quadratic function.

• example : Among all pairs of numbers whose difference is 8, find a pair whose product is a
minimum.

Let the numbers be x and y, with x the larger of the two. We know that x – y = 8. We want to
minimize the product P = x y. Make a substitution (y = x – 8) to write P as a function of one
variable.

P = x y = x (x –8) = x² − 8x

The minimum value of P occurs at x = –b/2a = – (–8)/2(1) = 4. When x = 4, y = 4 – 8 = –4.
The numbers are 4 and –4.

• example : You have 120 feet of fencing to enclose a rectangular region. Find the dimensions of
the rectangle that maximize the enclosed area.

Let the dimensions of the rectangle be x and y.

We know that 2x + 2y = 120.

We want to maximize the area. A = x y.

Write A as a quadratic function of one variable and determine where its maximum value occurs.

• example : Determine the equation of the parabola with vertex at ( 1, −2) and which goes through
the point ( 5, 3).

We know that h = 1 and k = −2, so the equation has the form f (x) = a(x −1)² − 2.

Since ( 5, 3 ) is on the graph, this point must satisfy the equation. We will use this fact to solve
for a.


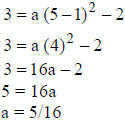
The equation of the parabola is