College Algebra Study Guide Exam 1
1. Determine whether the graph is that one of a function:
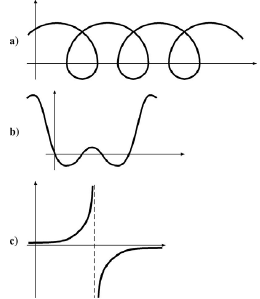
Example:
This is NOT a function, because the VLT shows us how the
vertical line hits the graph in
more than a point. For just a value of “x” we do have 3 values for “y” –
conclusion: this
is NOT a function.
2. Find the domain of the function:
Example:
b) The Domain of this function is: all Real numbers, but x can not be 5 or – 2.
Denominator can not be zero.
x2 – 3 x – 10 = 0. Factorize.
(x - 5)( x + 2) =0 Solve
x = 5 and x = -2
3. For the following functions use a grapher to estimate the domain and range:
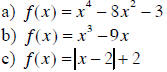
Example:
b) The Domain is all Real and the Range, the same, all Real. Notice that there
are no
restrictions for the Domain or Range.
c) If you graph you would realize that there are no restrictions for the Domain:
all Real,
but the Range will be [2, infinity).
4. Write a point-slope equation with the characteristics:
a) m = -2 and passing through (- 2, 4)
b) passes through (4, 1) and (-5, 7).
Example:
a) Use the point-slope form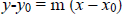 
, where
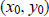are (-2, 4) and
the slope is m
= – 2. The point-slope form of the equation is y = - 2x
5. Determine whether the lines are parallel, perpendicular or neither:
a) y – 2x = 4 and 2y – 3 x = -7
b) 2y = 3x – 6 and 3y = -2x + 4
c) y = 6 and x = -2
Example:
b) Write the equations in the slope-intercept form so you would be able to see
the slope
of each. For the first one the form is y = (3/2)x – 3; the second one
is y = (-2/3)x + (4/3).
Because the product of the two slopes is – 1, the lines
are perpendicular.
6. Given the point (2, -3) and the line 3y – 2x = 4 find:
a) an equation parallel to the line and containing the point.
b) an equation perpendicular to the line and containing the point.
Example:
a) Write the equation of the line in the slope-intercept form y = (2/3)x +
(4/3). An
equation parallel with this one must have the same slope (2/3). Use
the point slope
equation where are (2, -3). Substitute. The equation
will be y = (2/3)x – (13/3)
7. Solve for x, and than graph:
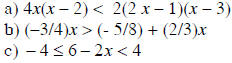
Example:
c) We need to isolate the x in the middle by subtracting (-6) an all 3 sides.
We will get:.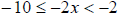 
Now divide everything by (-2)
in order to isolate x. Don’t
forget to flip the sign when you divide by a negative
coefficient!
We will get: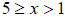 
or
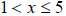
8. Fill the table and draw a graph for:
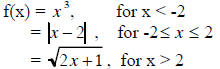
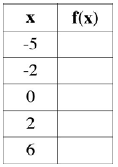
Example:
When x = -5 you substitute in f(x) = x3, the result is –125. For the next three
values (x = -
2, 0 and 2) you use the absolute value form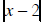 
, the results will
be 4, 2 and 0. The last
value, x = 6, you will use the radical form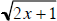 
, so the
.
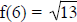9. Check the symmetries for the following functions:
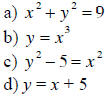
Example:
a) For the y-axis symmetry, substitute x with (-x); being at an even power the
result will
be unchanged, so the graph is symmetric with respect to y-axis.
For the x-axis symmetry, substitute y with (-y). The result will be the same so
the graph
is symmetric with respect to x-axis.
For the origin you will replace both (x, y) with (-x, -y). The result will be
the same, so the
graph is symmetric with respect to the origin. In fact, this is
the graph of a circle,
centered in the origin with the radius 3.
10. Test if the functions are even, odd or neither.
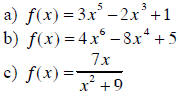
Example:
a) Substitute x with (-x). You will obtain
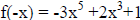. The function is NOT even
because f(-x) will not be f(x) and it is NOT odd because f(-x) is not -f(x) .
Conclusion is
"neither"
11. Each function is a translation of a simpler
function. Graph them both on a set of
coordinate axes.
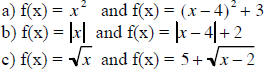
Example:
a) The vertex of the new graph would have the
vertex at (4,3) instead of (0,0). The new
graph would move 4 units to the right and 3 units up.
12. For the function
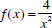and 
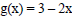find
:
a) domain of (f/g)
b) (f o g)(x)
c) (f/g)(-1)
Example:
b) We read ‘f compose with g' which means that you'll substitute (3-2x)
into f(x)
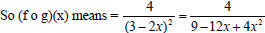
c) (f/g) (-1) – we substitute (-1) for x in both functions
and divide them. For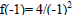 
= 4; g(-1)= 3 - 2(-1)= 5. (f/g) it is 4/5. The domain
of (f/g)(x) is all Real with the
exception of x=3/2; at x=3/2, g(x) will be zero .Which will make the new
function (f/g)
undefined.
13. Use a graphing calculator to find the intervals on
which the function is increasing or
decreasing .Consider the entire set of Real numbers if no domain is given:
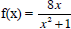
Example:
Graph the function using a normal window (-10,
10). You’ll see that the graph has y= 0
as an asymptote and is increasing only between (-1,1) and decreasing in rest
,
∞ )
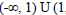14. Find the distance between (3,7) and (-2,4).
Find the midpoint between the same two
point.
Example:
You will use the distance equation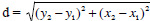 
,where
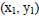is (3,7)
and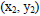 
is (-2, 4);
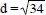. For the midpoint you will use the equation
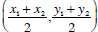; midpoint has
the coordinates (1/2, 11/2). Both formulas you may find
them in your calculator - if you don't have the programs, come to LC and you can
download them for free.
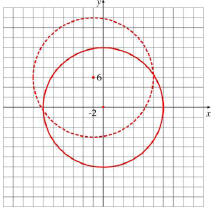
15. Find the equation of the circle with the center
(-2,6) and the radius 12 .Graph it.
Example:
The formula is (x – h)2 + (y – k)2 = R2, where h = -2, k = 6 and R is
12. The equation will
be (x + 2)2 + (y – 6)2 = 144. The graph of the
circle has the center moved from (0,0) to
(-2,6) -2 units to the left and 6 units up.
16. A word processor cost $555 when new and is expected to be
worth $80 after 5 years.
a) What is the worth after 3 years? b) A computer with
the same depreciation rate
cost $1280 when new . How much will it worth after 5 years ?
Example: Calculate the slope first: m = (80-555)/(5-0) =
-95$/year. Substitute the value
of t = 3 years in the equation C(t) = -95 t + 555 and
get the cost of C(3) = $270. The
computer with the same depreciation would have the same slope of -95$/year. The
equation will be C(t)=-95t +1280. Substitute the value t=5 and get C(5)=$805.