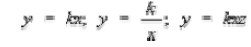Intermediate Algebra Online
COURSE
OBJECTIVES
At the end of the course, the student should have a working knowledge of the
following content areas:
1. Systems of equations.
2. Integral exponents and polynomials.
3. Linear and quadratic equations and linear inequalities.
4. Rational expressions and equations.
5. Radicals and rational exponents.
6. Introduction to functions.
Objective 1 The student will be able to
solve systems of linear equations.
1-1 – Solve a system of 3 linear equations in 3 unknowns using the addition
or substitution method.
1-2 – Solve an application problem using a system of linear equations.
Objective 2 The student will be able to apply
the laws of exponents and perform
operations using polynomials.
2-1 – Simplify an expression using the laws of exponents.
2-2 – Add, subtract and multiply polynomials.
2-3 – Divide a polynomial by a binomial using synthetic or long division.
2-4 – Factor polynomials by using various factoring techniques.
2-5 – Solve an equation by factoring.
2-6 – Solve an application problem that involves factoring.
Objective 3 The student will be able to solve
linear and quadratic equations and
linear inequalities.
3-1 – Solve an absolute value equation.
3-2 – Solve a linear inequality and show the solution set in interval
notation.
3-3 – Solve a compound linear inequality and show the solution set in
interval notation and graphical form.
3-4 – Solve an absolute value inequality and show the solution set in
interval notation and graphical form.
3-5 – Solve a quadratic equation by completing the square.
3-6 – Solve a quadratic equation by using the quadratic formula. The
following formula must be memorized:
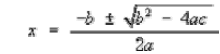
3-7 – Solve an application problem that involves the Pythagorean Theorem.
The following formula must be memorized:
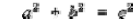
Objective 4 The student will be able to simplify
expressions and solve equations
containing rational expressions.
4-1 – Multiply or divide two rational expressions.
4-2 – Add or subtract two rational expressions.
4-3 – Simplify a complex fraction.
4-4 – Solve an equation containing rational expressions.
4-5 – Solve an application problem modeled by an equation that contains
rational expressions.
4-6 – Solve a formula for a specific variable.
Objective 5 The student will be able to simplify
expressions and solve equations
containing rational exponents and radicals.
5-1 – Simplify a radical expression.
5-2 – Evaluate and simplify an expression containing rational exponents.
5-3 – Add or subtract radical expressions.
5-4 – Multiply radical expressions.
5-5 – Simplify a radical expression by rationalizing the denominator.
5-6 – Solve equations using even- and odd-root properties.
5-7 – Solve an equation containing radicals.
5-8 – Solve an equation containing rational exponents.
5-9 – Add, subtract, multiply or divide complex numbers.
5-10 – Find the distance and midpoint between two given points. The
following formulas must be memorized:

Objective 6 The student will be able to
understand the basic language and notation of
a function.
6-1 – Find the equation in both standard and slope-intercept form of a
straight line through two given points. The following formulas must
be memorized:
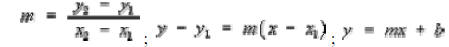
6-2 – Find the equation in both standard and slope-intercept form of a
straight line that is parallel or perpendicular to a given line through a
given point.
6-3 – Determine whether a given equation or graph is a function or a
relation.
6-4 – Determine the domain and range of a function or relation.
6-5 – Evaluate or simplify an expression from function notation.
6-6 – Graph a parabola, stating the vertex, axis of symmetry, domain and
range, intercepts, and minimum/maximum. The following formula
must be memorized:
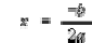
6-7 – Graph a circle by first finding its center and radius.
6-8 – Solve an application problem involving quadratic functions.
6-9 – Set up and solve a variation problem. The following formulas must be
memorized: