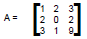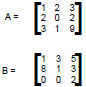| The Computing Engine
 Matlab is a
calculator on Steroids Matlab is a
calculator on Steroids
 Has hundreds of built-in mathematical Has hundreds of built-in mathematical
functions that are built upon efficient
algorithms
 Some simple examples: Some simple examples:
 Numerically computes most calculus concepts Numerically computes most calculus concepts
such as derivatives and integrals
 Matrix operations such as numerically solving Matrix operations such as numerically solving
complex systems of equations
|
Quick Intro to Variables
 Variables Variables
 Like on your TI-83, you can assign variables to Like on your TI-83, you can assign variables to
remember answers, objects, and user input.
 Example in Matlab: Example in Matlab:
 x = 3; x = 3;
 Note: the semicolon suppresses the output on the command Note: the semicolon suppresses the output on the command
line, try x = 3 without it and you will see!
 Now you can use this variable x later in different Now you can use this variable x later in different
mathematical operations (if used in the command line
window, it is a global variable meaning it can be used
anywhere in Matlab)
 Keep track of your variable names!!!!! Keep track of your variable names!!!!! |
| Let’s add some numbers…
 2 + 2 on the
command line 2 + 2 on the
command line
 See the
answer that comes out See the
answer that comes out
(hopefully 4)
 The ans
variable The ans
variable
 Stands for “answer” Stands for “answer”
 Default variable for all common unassigned Default variable for all common unassigned
operations done in command line window
 See how it appears in the variable See how it appears in the variable
workspace window? |
Order of Operations
 PEMDAS
PEMDAS
 “Please Excuse My Dear Aunt Sally” “Please Excuse My Dear Aunt Sally”
 Parentheses, Exponent, Multiplication Parentheses, Exponent, Multiplication
Division, Addition, Subtraction
 Try it out:
Try it out:
 2 + 2 / 4 = 2.5 2 + 2 / 4 = 2.5
 (2 + 2) / 4 = 1 (2 + 2) / 4 = 1
|
| Matlab and Matrices
 The name Matlab
The name Matlab
 “Matrix Laboratory” “Matrix Laboratory”
 Originally an open application that came out Originally an open application that came out
of the Argonne government research
institution (free!)
 Initially designed for doing complex
Initially designed for doing complex
algorithms involving matrices in linear
algebra and engineering applications |
Matrices in Matlab
 A foundational
programming type A foundational
programming type
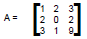
 Representing it in Matlab: Representing it in Matlab:
 A = [1 2 3; 2 0 2; 3 1 9] A = [1 2 3; 2 0 2; 3 1 9]
 Semi-colons mean new lines, spaces between numbers Semi-colons mean new lines, spaces between numbers
represent row placement (you can also use commas) |
| More Matrices
 Keep in mind that
a matrix can be a Keep in mind that
a matrix can be a
single row! Some call this a vector.
 A 3
element row-vector ( a 1x3 matrix) is A 3
element row-vector ( a 1x3 matrix) is
easy to type out, but what if you need a
100 element row-vector?
 Try the
syntax: Try the
syntax:
 t = 1:100 or t = 1:100 or
 t = 1: 1: 100 t = 1: 1: 100
 What if you did “t = 1 : 0.01 : 100” ? What if you did “t = 1 : 0.01 : 100” ? |
Matrix Operations
 Multiply a 3 x 3
Matrix with another: Multiply a 3 x 3
Matrix with another:
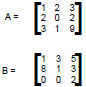
 A x B A x B
|
| Built-in Matlab Functions
 Determinant of
our Matrix A Determinant of
our Matrix A
 det(A) det(A)
 Inverse of
our Matrix B Inverse of
our Matrix B
 inv(B) inv(B)
|
Built-in Matlab Functions
 Some more basic
operations: Some more basic
operations:
 sqrt(4) – takes a square root of a number sqrt(4) – takes a square root of a number
 mod(4,3) – modulus (we will use this later) mod(4,3) – modulus (we will use this later)
 reciprocal(5) – gives the reciprocal of a number reciprocal(5) – gives the reciprocal of a number
 cos(t) – gives the cosine of variable t cos(t) – gives the cosine of variable t
 Note: if t is a row-vector, Matlab is adept enough to Note: if t is a row-vector, Matlab is adept enough to
recognize that it should take the cosine of each element
in t, and returns a row vector that is same length of t
 exp(4) – represents e4 exp(4) – represents e4
 log(4) – represents the natural log of 4 ( ln(4) ) log(4) – represents the natural log of 4 ( ln(4) ) |
| Exercise!
 Assign variables
x, y, a, b for different Assign variables
x, y, a, b for different
values of a sine function
 Put these
variables into a row-vector A Put these
variables into a row-vector A
 Plot A
over a domain of 4 values Plot A
over a domain of 4 values
 Get a good
representative plot of a sine Get a good
representative plot of a sine
function
 Improve the “resolution” by
specifying more Improve the “resolution” by
specifying more
values for the independent variable |
|



 Matlab is a
calculator on Steroids
Matlab is a
calculator on Steroids Has hundreds of built-in mathematical
Has hundreds of built-in mathematical Numerically computes most calculus concepts
Numerically computes most calculus concepts Note: the semicolon suppresses the output on the command
Note: the semicolon suppresses the output on the command