Scientific Computing Lecture 5 - Matrix Operations 1
| Overview
|
|
Matrix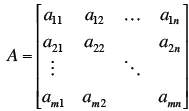 |
Submatrice
|
| Partitioning
|
Special Matric
|
| More Special Matrices
|
Matrix Addition
|
| Run Time of Matrix Addition
|
Is Matrix or Vector Addition Faste
|
| Row Major and Column Major
|
Loop Nesting
|
| Matrix Norms
|
Special Matrix Norms
|
| Matrix Vector Product
|
Alternative Computation
|
| Run Time Analysis
|
Run Time Analysis (ii)
|



 Definitions
Definitions Matlab does this (everything is a
matrix in matlab)
Matlab does this (everything is a
matrix in matlab)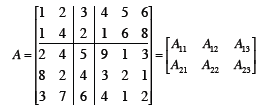
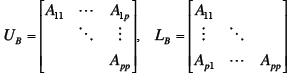
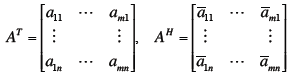
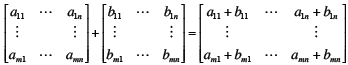
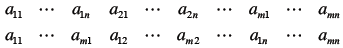
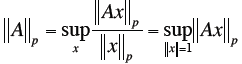
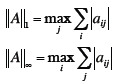
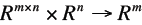
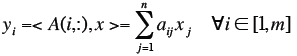
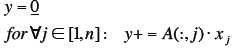
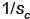 mn
memory loads and
mn
memory loads and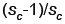 mn loads
mn loads