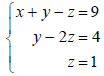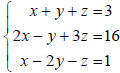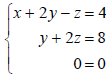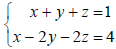More Algebra Help

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Multivariable Linear Systems

Objective:
In this lesson you learned how to recognize linear systems in
row-echelon form and to use back-substitution to solve the
systems, how to solve systems of equations by Gaussian
elimination, how to solve nonsquare systems of equations,
and how to use systems of linear equations in three or more
variables to model and solve real-life problems.

Important Vocabulary Define each term or concept.

Row-echelon form

Ordered triple

Row operations a

Gaussian elimination

Nonsquare system of equations

I. Row-Echelon Form and Back-Substitution (Page 687) When elimination is used to solve a system of linear equations, the goal is. . . Example 1: Solve the system of linear equations.	What you should learn How to use back- substitution to solve linear systems in row- echelon form
II. Gaussian Elimination (Pages 688-691) To solve a system that is not in row-echelon form, . . . List the three row operations on a system of linear equations that produces an equivalent system of linear equations. 1. 2. 3. The solution(s) of a system of linear equations in more than two variables must fall into one of the following three categories: 1. 2. 3, Example 2: Solve the system of linear equations. Example 3: The following equivalent system is obtained during the course of Gaussian elimination. Write the solution of the system	What you should learn How to use Gaussian elimination to solve systems of linear equations

III. Nonsquare Systems (Page 692) In a square system of linear equations, the number of equations in the system is __ the number of variables. If a system has more variables than equations, the system cannot have a(n) ___ . Example 4: Solve the system of linear equations.	What you should learn How to solve nonsquare systems of linear equations

IV. Applications of Multivariable Systems (Pages 693-694) The height at time t of an object that is moving in a vertical line with constant acceleration a is given by the position equation ____ , where s is measured in feet, t is measured in seconds, v₀ is the initial velocity, and s₀ is the initial height. Describe a situation or application in which solving a system of multivariable linear systems is required. Example 5: Find a quadratic equation, y = ax ² + b x + c , whose graph passes through the points (- 4, 36), (0, 8), and (2, 0).	What you should learn How to use systems of linear equations in three or more variables to model and solve application problems

Additional notes

Homework Assignment

Page(s)

Exercises

We Promise to Make your Math Frustrations Go Away!

More Algebra Help

Multivariable Linear Systems