Solving Quadratic Equations by Factoring

Quadratic equations are equations (not just polynomials) of the second-degree, that is, they have
an x² term in them. Examples are: x² + x = 5 and x² – 2x + 35 = 0.

The standard form of a quadratic equation is: ax² + bx + c = 0.

To solve the quadratic equation x² + 7x + 6 = 0, we must find the values of x that make this
equation true. We can do this by factoring.

Factoring a polynomial gives us a product of factors:

x² + 7x + 6 = (x + 6)(x + 1)

If a product of two numbers equals zero, for example, ab = 0, then either a must equal zero or b
must equal zero (because anything multiplied by zero equals zero), or both may equal zero. This
is called the principle of zero products.

So, if (x + 6)(x + 1) = 0, then either (x + 6) = 0 or (x + 1) = 0. To solve the original equation, we
solve for x in both of these equations:

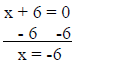
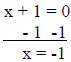
The solutions for x² + 7x + 6 = 0 are –6 and –1.

If the polynomial turns out to be a perfect square, you only get one solution (or really the same
solution twice):

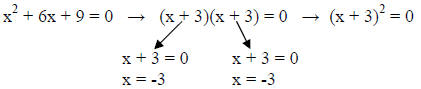
The solution is x = -3. In this case, both factors will equal zero when x = -3.

Solving a Quadratic Equation

Step 1: Make sure all terms are on
one side of the equation and zero is
on the other side.

a. x² – 7x = -12 → x² – 7x + 12 = 0

b. 5x² = 15x → 5x² – 15x = 0

c. x(x - 6) = 27 → x(x - 6) – 27 = 0

d. (2x + 5)(x + 9) = 15 → (2x + 5)(x + 9) – 15 = 0

Step 2: If some terms were written
in factored form originally, do all the
multiplication and combine like terms.

c. x(x - 6) – 27 = 0 → x² – 6x – 27 = 0

d. (2x + 5)(x + 9) – 15 = 0
→ 2x² + 23x + 45 – 15 = 0
→ 2x² + 23x + 30 = 0

Step 3: Factor and solve by setting each factor equal to zero:

a. x² – 7x + 12 = 0

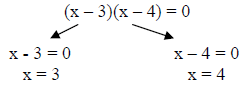
The solutions are x = 3 or x = 4.

b. 5x² – 15x = 0

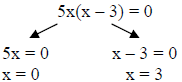
The solutions are x = 0 or x = 3.

c. x2 – 6x – 27 = 0

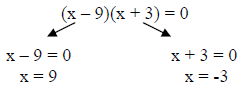
The solutions are x = 9 or x = -3.

d. 2x² + 23x + 30 = 0

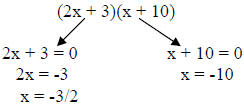
The solutions are x = -3/2 or x = -10.

So why are we doing this?

This section is an introduction to topics in Math 102 – problem solving using quadratics and
graphing quadratic functions. Quadratic functions are useful when we are trying to find the
maximum or minimum of a function, such as maximizing area or minimizing cost. These topics
will be covered later.

The graph of a quadratic function is called a parabola and looks like these:

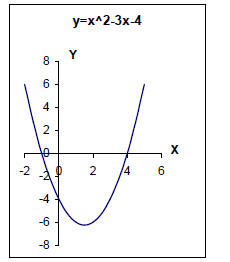
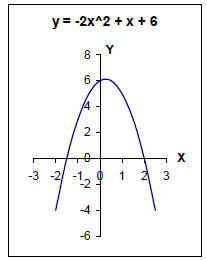
With what you know now, you can find the x-intercepts of these graphs. The x-intercepts are
where the graph crosses the x-axis. At these points, y = 0. (In Section 3.2, you looked at the
y-intercept of straight-line functions - where the line crossed the y-axis. This concept is similar.)
When you solve a quadratic equation, you are finding the x-intercepts of the quadratic function
(called finding the “zeros” or “roots”).

For the graphs above:

y = x² – 3x – 4
y = -2x² + x + 6

Set y = 0:

0 = x² – 3x – 4
0 = -2x² + x + 6

Factor and solve:

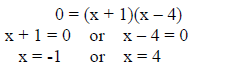
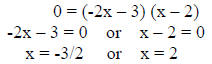
Using these values of x, and remembering y = 0, we can state these values as ordered pairs of
coordinates on a graph in the form (x, y). These represent the points on the graphs which are the
x-intercepts:

x = -1, y = 0 and x = 4, y = 0
x-intercepts: (-1, 0) and (4, 0)

x = -3/2, y = 0 and x = 2, y = 0
x-intercepts: (-3/2, 0) and (2, 0)

And you can see above, these points are where the graphs cross their x-axes.

Exercises:
Solve, using the principle of zero products:

1. (x + 3)(x + 11) = 0
2.

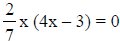
3. (x – 7)(x + 75)(x – 43) = 0

4. 0.35x (0.1x + 0.4)(0.05x – 15) = 0

Solve by factoring:

5. 9x² – 16 = 0
6. x² + 7x = 18
7. 3x² – 10x – 8 = 0
8. 36x² +84x + 49 = 0
9. 15x² +10x = 0
10. (5x + 3)(x – 1) = 13

Find the x-intercepts:

11. y = x² – 6x + 9
12. y = -3x² +5x + 2

Answers:

1. x = -3 or –11
2. x = 0 or ¾
3. x = 7 or –75 or 43
4. x = 0 or –4 or 300
5. x = 4/3 or –4/3
6. x = -9 or 2
7. x = -2/3 or 4
8. x = -7/6
9. x = 0 or –2/3
10. x = -8/5 or 2
11. (3, 0)
12. (-1/3, 0), (2, 0)