Sums and Differences of Rational Functions

→ Example 13. Simplify the expression

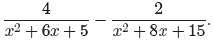
State all restrictions.

First, factor each denominator.

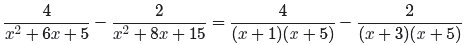
The least common denominator, or least common multiple (LCM), requires that we
write down each factor that occurs, then affix the highest power of that factor that
occurs. Because all factors in the denominators are raised to an understood power of
one, the LCD (least common denominator) or LCM is (x + 1)(x + 5)(x + 3).

Next, we make equivalent fractions having this common denominator.

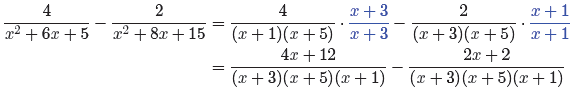
Subtract the numerators and divide by the common denominator. Be sure to use
grouping symbols, particularly with the minus sign that is in play.

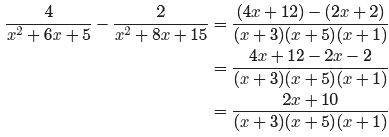
Finally, we should always make sure that our answer is reduced to lowest terms.
With that thought in mind, we factor the numerator in hopes that we can get a common
factor to cancel.

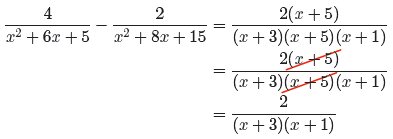
The denominators have factors of x+3, x+5 and x+1, so the restrictions are x = −3,
x = −5, and x = −1, respectively. For all other values of x, the left-hand side of

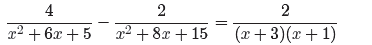(14)

is identical to its right-hand side. Again, this is easily tested using the table feature of
the graphing calculator, as shown in the screenshots in Figure 3. Again, note the ERR
(error) messages at each restricted value of x, but also note that Y1 and Y2 agree for
all other values of x.

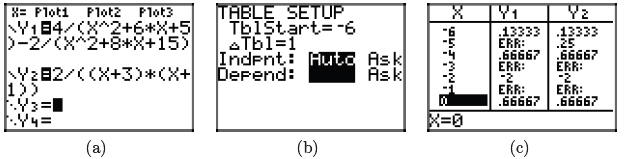
Figure 3. Using the table feature of the graphing calculator to check the result in
equation (14).

Let’s look at another example.

→ Example 15. Simplify the expression

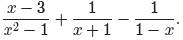
State all restrictions.

First, factor all denominators.

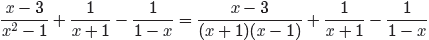
If we’re not careful, we might be tempted to take one of each factor and use (x+1)(x−
1)(1−x) as a common denominator. However, let’s first make two negations of the last
of the three fractions on the right, negating the fraction bar and denominator to get

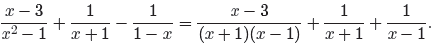
Now we can see that a common denominator of (x + 1)(x − 1) will suffice. Let’s make
equivalent fractions with this common denominator.

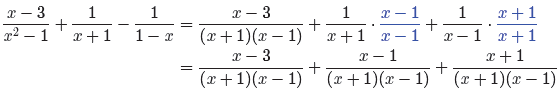
Add the numerators and divide by the common denominator. Even though grouping
symbols are not as critical in this problem (because of the plus signs), we still think it
good practice to use them.

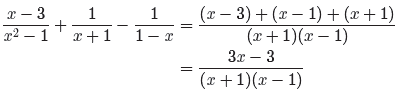
Finally, always make sure that your final answer is reduced to lowest terms. With
that thought in mind, we factor the numerator in hopes that we can get a common
factor to cancel.

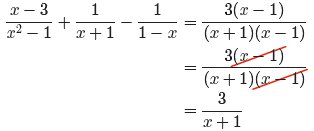
The factors x + 1 and x − 1 in the denominator produce restrictions x = −1 and
x = 1, respectively. However, for all other values of x, the left-hand side of

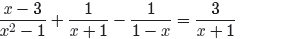(16)

is identical to the right-hand side. Again, this is easily checked on the graphing calculator
as shown in the sequence of screenshots in Figure 4.

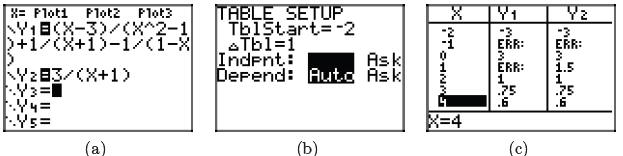
Figure 4. Using the table feature of the graphing calculator to check the result in
equation (16).

Again, note the ERR (error) messages at each restriction, but also note that the values
of Y1 and Y2 agree for all other values of x.

Let’s look at an example using function notation.

→ Example 17. If the function f and g are defined by the rules

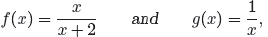
simplify f(x) − g(x).
First,

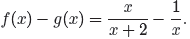
Note how tempting it would be to cancel. However, canceling would be an error in this
situation, because subtraction requires a common denominator.

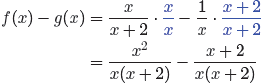
Subtract numerators and divide by the common denominator. This requires that we
“distribute” the minus sign.

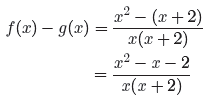
This result is valid for all values of x except 0 and −2. We leave it to our readers to
verify that this result is reduced to lowest terms. You might want to check the result
on your calculator as well.