The Real Numbers

What are the real numbers? As explained in the introduction to Chapter 3, there are two
approaches to answering this question. One approach would be to construct the set R of real
numbers starting with the set N of natural numbers. Along the way, we would need to construct
the set Z of integers and the set Q of rational numbers.

The other approach—the one followed here—is not to say what the real numbers are, but
only to describe how they behave. In other words, our approach is to state, in the form of
axioms, the fundamental properties of the set of real numbers.

Our axiomatic approach does not, of course, establish that any set having these properties
actually exists! To establish that one needs to take a constructive approach. But the axiomatic
approach does uniquely characterize the set of real numbers in the sense that any two sets
having these properties are "essentially" the same (in technical terms, they are "order isomorphic"
as ordered fields). This essential uniqueness is established in Section 3.4. However, in
this course we shall not look into the matter of uniqueness of R.

The axioms for R can be summarized as follows:

R is an ordered field that includes N, has the Archimedean Ordering Property,
and has the Nested Interval Property.

To say that R is a field means that there are operations of addition and multiplication in
R with "the usual" algebraic properties. These algebraic properties are listed in Axioms 3.1.4.
In particular, each  x ∈ R has a negative -x for which x + (-x) = 0, and each nonzero y ∈ R
has a multiplicative inverse y ^-1 for which yy ^-1 = 1. Then subtraction and division of real
numbers may be defined by x - y = x + (-y) and, for y ≠ 0, x/y = xy ^-1.

Beyond those basic properties we shall assume without proof all the familiar algebraic properties
listed in Proposition 3.1.12.

To say that the field R is ordered means that there is a relation < in R having "the usual"
algebraic properties such as those listed in Proposition 3.2.4. Among these properties are the
following:

• For each  x ∈ R, exactly one of the relations 0 < x, x = 0, and x < 0 holds.

• For all x,y ∈ R, x < y 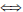0 < y - x.

• For all x,y ∈ R, if 0 < x and 0 < y, then 0 < x + y and 0 < xy.

From just these three properties all the other familiar properties of order for real numbers
(as listed in Proposition 3.2.4) can be deduced. Here’s an example: For all x,y, z ∈ R,

x < y =>x + z < y + z.

In fact, assume x < y. This means 0 < y - x. But y - x = (y + z) - (x + z). Thus 0 <
(y + z) - (x + z). This means x + z < y + z.

Exercise 1. Using just the properties of ordering listed above together with the usual algebraic
properties of addition and multiplication, deduce:

(a) If 0 < x, then -x < 0.

(b) If x < y, then -y < -x.

(c) 0 < 1

When we say here that R "includes" N, we do not mean merely that N R. Rather, we mean
also that:

• if m,n ∈ N, then their sum m+ n and product m· n as elements of R are the same as
their sum and product, respectively, as natural numbers [as defined in Example 1.2.10 (2)
and Exercise 1.2.11 (3)];

• the number 0 ∈ N is the identity element for addition in the field R and the number 1 ∈ N
is the identity element for multiplication in the field R; and

• if m,n ∈ N, then the relation m < n holds for m and n as elements of R if and only if it
holds for them as elements of N [as defined in Exercise 1.2.11 (2)].

With N as a subset of R, the set Z of all integers and the set Q of all rational numbers may
be defined as:



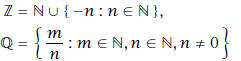
The Archimedean Ordering Property of the ordered field R is the following:

For every ε  ∈ R with ε > 0 and for each c  ∈ R, there exists a positive integer n such
that nε > c.

This property may be expressed by saying that if you take a real number c, no matter how
large, and a positive real number ε, no matter how small, then if you add ε to itself enough
times, the sum will be greater than c.

For more about the Archimedean Ordering Property, see Section 3.2.

Proposition 2. Let c ∈ R. Then there exists a unique n ∈ Z for which n ≤ c < n + 1.

Proof. Existence. Case (i): c ≥ 0. By the Archimedean Ordering Property, there exists some
k ∈ N such that k · 1 > c. By the Well-Ordering Principle for N, there is a least such k; call it
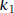. Let 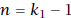. Then n ≤ c < n + 1 (why?).

Case (ii): c < 0. Then -c > 0 and so, by what was just proved, there exists an integer m
with m ≤ -c < m+ 1. Then …(finish the existence proof in this case.)

Uniqueness. Exercise.

Theorem 3 (Order Density of Q in R). If a, b ∈ R with a < b, there exists some q ∈ Q for which
a < q < b.

Proof. See the proof of Theorem 3.2.27. In that proof, just change F to R, Q(F) to Q, and N(F)
to N.

For real numbers a and b, as usual the closed interval [a, b] is the set { x ∈ R : a ≤ x ≤ b}.
The Nested Interval Property of R is the following:

If 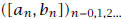is a sequence of closed intervals in R that is decreasing in the
sense that 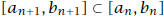or each n = 0, 1, 2, . . . , then .

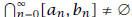For more about the Nested Interval Property, see Section 3.3.
We already know there is no rational number c for which c² = 2. One of the consequences
of the Nested Interval Property is that there is some real number c for which c² = 2 or, as we
shall say, that 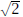exists.

With the theory of calculus at our disposal this would be easy to prove: see Exercise 4

Exercise 4. Prove that 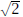exists by applying the Intermediate Value Theorem to the function
f : R → R given by f (x) = x².

For the method in Exercise 4, you need to know that the function f is continuous (and
so you need to know a precise definition for "continuous"); you also need to know have the
Intermediate Value Theorem at your disposal. So we shall not use such a proof.

That 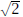exists is proved by an indirect method in Section 3.3, namely, by first deducing
from the Archimedean Ordering Property and the Nested Interval Property that each nonempty
subset of R that is bounded above has a least upper bound.

In this note we give a different proof that directly invokes the Archimedean Ordering Property
and the Nested Interval Property. In following the proof it may help if you draw a diagram
with a line representing R and mark on it the points and intervals constructed. Be sure to
supply any missing justifications for steps.