Musings on Factoring of Polynomials
The factoring of polynomials (1) is a topic in algebra
about which students have vastly different feelings:
• for some, factoring is a prime example of a technique for which the most
appropriate response is, "When
are we ever gonna use this?.
• for some others, factoring provides an enjoyable puzzle, akin, perhaps,
to diagramming sentences in an English
class.
I should be explicit about the difference between factoring a polynomial, such
as x2 - 5x +6 =(x - 2)(x - 3) and
factoring an integer, such as 629 = 17 · 37.
 |
In the first example, the equals sign means that,
for every x, the value of the polynomial, x2 – 5x – 6, for any number x, equals the product of the numbers, x – 2 and x – 3, for that number x, and so there are infinitely many numerical equalities contained in the single algebraic equation; while, in the second example, we are told that the number, 629, equals (or can be expressed as, or can be factored into) the product of the two numbers, 17 and 37. Few students see any significance in factoring, and many teachers join students in disdain or distaste for factoring. Sandie Coelho, PIMMS’ former Associate Director for Mathematics, showed me a sheaf of questions and answers about what’s factoring good for? or why teach factoring?—the teacher-discussants were seriously trying to find justification for their teaching of a topic that they feared has no significance. In that sheaf, not one person could provide a reason for learning how to factor polynomials! |
Indeed, one frustrated respondent said that, if asked by a
student, "What good is it to know how to factor x2 – 5x – 6?",
he would answer,
"Factor this expression or I’ll pull the trigger of this loaded pistol that I’m
holding to your temple." This
mean Dickensian teacher isn’t much worse than the sarcastic Euclidean mentor who
tells his assistant to give a dime to the
student "since he needs to have some reason to study."
If I am asked, "Should students in a high school algebra class spend substantial
time to learn factoring of polynomials?",
I respond with a clear-cut "NO and
YES." Let me explain:
If the student’s experience with factoring embodies no more than a semi-infinite
number of problems like the following:
"By factoring, solve the equation 168 +
15x – 18x2 = 0,"
then the student has been cheated.
It is desirable, of course, for the student to realize that
•168 + 15x – 18x2 =
3(56 + 5x – 6x2);
•168 + 15x – 18x2 = 0  56 + 5x – 6x2 =0; that is, the two
quadratic equations have the same solutions and
56 + 5x – 6x2 =0; that is, the two
quadratic equations have the same solutions and
therefore are equivalent;
•
For
real p, q, p· q = 0  p = 0, or q = 0, or both;
p = 0, or q = 0, or both;
•
If, for all real numbers, x, 56 +
5x – 6x2 = (a + bx) (c + dx) for integers a, b, c, d,
then ac =56 and bd = – 6; and
•
There are only finitely many values of a, b, c, d
that need be tested to find the possible factors.
Many students do not appreciate any of the statements contained in the foregoing
bullets. Consider the amusing
blunder made by some students in applying bullet
#3:
Asked to solve 56 + 5x – 6x2 =0 , the student (correctly) rewrites the equation
as: 6x2 – 5x = 56,
permitting the factorization: x(6x – 5) = 56.
Now the student applies a home-grown (and false) generalization of our
"fundamental principle" (bullet #3) to
conclude that
x = 56 or 6x – 5 = 56 (!)
The student failed to recognize that the statement of bullet #3 is true if and
only if the constant is zero.
To teach factoring as a method for solving quadratic equations may be considered
an exercise in futility, because
the factorable quadratic expressions form so
insignificant a subset of all quadratic expressions.
But, "completing the square" to obtain the "quadratic formula"—now there’s
something worthwhile! I say this with
enthusiasm because the process of
completing the square leads to reducing the quadratic equation whose roots we
seek to
a couple of linear equations whose roots we already know how to find—in analogy
with the sort of reduction used by Tart-
aglia and Ferrari to solve cubic
and quartic equations (2). Often the solutions (answers) of a problem are almost
unrelated to
the value of solving the problem. The important values of solving classroom
problems are the procedures (patterns, or sequences
of steps) that
are recognized as useful also in solving numerous other problems.
In response to the query, "When are we ever gonna use this?", the student
probably expects an example that seems
practical, from his or her point of view,
and solving an algebraic equation does not strike the average ninth-grader as a
really
urgent matter. In calculus, factoring is useful to break a rational
fraction expression into partial fractions, permitting us to
integrate the
original expression and to deal with some infinite series. But, for a high
school teacher to appeal to these applications
as reasons for learning to
factor forces the teacher to say, "Trust me, you’ll need this sometime in the
future"—a
pedagogically weak argument (3).
Thus, I say NO! to spending lots of time in elementary and intermediate algebra
classes on factoring quadratic expressions
in order to solve quadratic
equations.
On the other hand, I think that it is not only desirable but really
pedagogically necessary to work through some factoring to
get across the
important concepts contained in the five bullets above. This explains part of
the reason for the YES in my answer
to the factoring question.
Now let me strengthen my YES by outlining three problems, not involving the
solution of equations, whose solutions
require that students have an
understanding of factoring and some facility with the process. The first of
these problems
is appropriate for a first course in algebra, while the second
and third may require more mathematical maturity than typical
ninth-graders
have.
Prob. 1
Observe that
1 ∙ 3 + 1 = 4,
2 ∙ 4 + 1 = 9,
3 ∙ 5 + 1 = 16,
4 ∙ 6 + 1 = 25,
5 ∙ 7 + 1 = 36.
What pattern do you notice? Express your guess (conjecture) in words. How do you
know whether
this pattern continues indefinitely?
The pattern might be described as follows: The product of two consecutive odd
numbers, or of two consecutive even numbers,
plus 1, equals a perfect square -
the square of the “skipped” number.
A direct algebraic argument that this pattern is valid in general follows from
letting the first number in the product be
called n. It doesn’t matter whether
it is even or odd. Then the second number in that product will be n + 2; the
product
of the two numbers is n(n + 2); and the left hand side of the equations
of the problems will be n(n + 2) + 1.
But n(n + 2) + 1 = n2 + 2n + 1, which equals (n + 1)2.
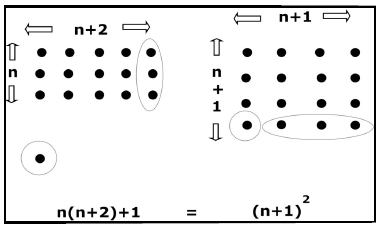 |
This is clearly the square of (n + 1), the number
"skipped" between n and (n + 2). The equality n(n + 2) + 1 = (n + 1)2 is an identity, valid for all integers, n, and thus validates the guess expressed in words above. |
Prob. 2 (Given to a Middletown, CT sixth-grade class by
the cosmopolitan mathematician and educator, W. W.
Sawyer, over 50 years ago.
The problem also appears as the second exercise in The Theory of Numbers, a text
written by the
noted American mathematician, Robert D. Carmichael, about 100
years ago.)
Observe that
1 ∙ 2 ∙ 3 ∙ 4 + 1 = 25,
2 ∙ 3 ∙ 4 ∙ 5 + 1 = 121,
3 ∙ 4 ∙ 5 ∙ 6 + 1 = 361, and
4 ∙ 5 ∙ 6 ∙ 7 + 1 = 841.
What pattern(s) do you notice? Express your guesses (conjectures) in words.


