Geometry Form A

1. The hypotenuse of a right triangle is
12" long, and one of the acute angles
measures 30 degrees. The length of
the shorter leg must be:

(A) 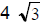inches (B) 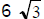inches
(C) 5 inches (D) 6 inches
(E) 7 inches

2. The sum of the measures of all of the
non-overlapping angles formed by 7
rays drawn on the same side of a line
from the same point of that line is (?)

(A) 1260° (B) 1080° (C) 900°
(D) 360° (E) 180°

3. How many degrees are there in an
angle that measures one-ninth of its
complement?

(A) 810° (B) 162° (C) 81°
(D) 80° (E) 9°

4. Each interior angle of a regular
octagon is:

(A) 120° (B) 144° (C) 135°
(D) 140° (E) 108°

5. ABCD is a rhombus with BC = 5, and
BD = 6. What is the length of CA?

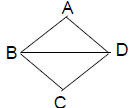
(A) 8 (B) 9 (C) 10
(D) 11 (E) 12

6. Which of the following is true if two
given triangles are not similar?

(A) their areas cannot be equal
(B) they may be congruent
(C) they are not congruent
(D) their corresponding sides may
be proportional
(E) their corresponding angles may be
equal

7. The points (1,2), (- 4,3) and (7,- 6) are
three vertices of a parallelogram. The
fourth vertex is:

(A) (12,- 2) (B) (2,- 11)
(C) (- 11,5) (D) all of these
(E) none of these

8. A triangle and a rectangle have equal
areas. The base and height of the
triangle are 12 and 4, respectively.
Find the width of the rectangle if its
length is 8.

(A) 3 (B) 4 (C) 5
(D) 6 (E) 7

9. A rectangle has length x units and
width y units. The rectangle has the
same perimeter as an equilateral
triangle with a side of m units.
Find x in terms of m and y.

(A) m + y (B) m - y
(C) 3m - 2y
(D) 1/2m + y (E) 1/2(3m - 2y)

10. The side of a cube is decreased by
50%. By how much does the volume
decrease?

(A) 12.5% (B) 25% (C) 50%
(D) 75% (E) 87.5%

11. If the circumference of a circle is 12π
feet, what is the number of square feet
in its area?
(A) 6π (B) 9π (C) 36π
(D) 81π (E) 144π

12. What is the area of a circle inscribed
in a square that has a side length of
8 cm?

(A) 8π cm² (B) 16π cm² (C) 32 π cm²
(D) 64π cm² (E) 48π cm²

13. In circle C, minor arc XK is 1 / 3 of the
circumference of the circle. If F is not
on minor arc XK, what is the measure
of inscribed angle XFK ?

(A) 60° (B) 30° (C) 15°
(D) 120° (E) 300°

14. Find the area of the shaded part of the
figure:

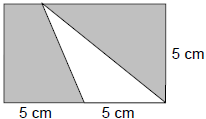
(A) 25cm² (B) 50cm² (C) 35cm²
(D) 37.5 cm² (E) 12.5 cm²

15. If a quadrilateral is inscribed in a
circle, the opposite angles are:

(A) congruent (B) obtuse
(C) complementary (D) acute
(E) supplementary

16. A circle can be inscribed in:

(A) any triangle (B) any octagon
(C) any trapezoid (D) any polygon
(E) any parallelogram

17. The area of a trapezoid is 160 square
units, one base is 26 units, and the
height is 8 units. What is the length of
the other base?

(A) 7 (B) 14 (C) 56
(D) 6 (E) 80 / 17

18. A square piece of paper, with one side
equal to 12 units, is folded so that the
four corners of the square meet in the
center of the square. This forms a new
square. What is the side measure of
the new square?

(A) 5 (B) 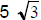(C)
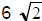
(D) 6 (E) 8

19. The diameter of the front wheel of a
tricycle is 8" and the diameter of each
rear wheel is 3". How many
revolutions has each back wheel
made while the front wheel has
turned 1440 degrees?

(A)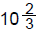
(B) 4 (C)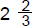
(D) 24 (E) 96

20. A circular track has a radius of 210
feet. Approximately how many times
must a jogger circle the track in order
to jog one mile?

(A) 20 (B) 4 (C) 35
(D) 39 (E) 34

21. The value of B is:

(A) 3.14 (B) 3.1415
(C) 3.141592 (D) 3.1415926535
(E) none of these

22. The area of a circle inscribed in an
equilateral triangle is 4p. What is the
height of the triangle?

(A) 2 (B) 4 (C) 6
(D) 8 (E) 10

23. The sum of the exterior angles of any
polygon will always be what measure?

(A) 180°
(B) 360°
(C) (n – 2) 180°
(D) (n + 2) 180°
(E) none of these

24. The area of a square 18 ft. on a side
is equal to the area of a rectangle
with a length of 3 yards. The width of
this rectangle is:

(A) 2 ft. (B) 9 ft. (C) 18 ft.
(D) 36 ft. (E) 27 ft.

25. The set of points in a plane at a fixed
distance from a given point in that
plane is:

(A) a line (B) a circle (C) an angle
(D) two lines (E) a point

26. The radii of two circles are 3 cm and
5 cm, respectively. Find the radius of
the circle whose area is equal to the
sum of the areas of the two given
circles.

(A) 8 (B) 34 (C)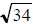
(D) 34π (E) none of these

27. Three lines lie in one plane. Line m
intersects line n which is parallel to
line p. How many points are
equidistant from all three lines at the
same time?

(A) 2 (B) 1 (C) 0
(D) 4 (E) 8

28. A sector of a circle has the same area
as an equilateral triangle whose base
is 12. What is the area of the sector?
(A)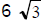 (B) 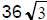(C) 12
(D) 144 (E) none of these

29. The number of points on a circle that
are equidistant from the endpoints of a
given diameter is:

(A) 1 (B) 2 (C) 3
(D) 4 (E) 5

30. The radius of a circle is increased by
50%. By how much does the area
increase?

(A) 25% (B) 50% (C) 100%
(D) 125% (E) 250%

31. In the figure, AB = AC, DB = DC,
πABC = ½ πDBC, and pD = 70°.
How many degrees are there in πA?



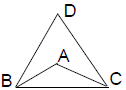
(A) 55 (B) 70 (C) 105
(D) 110 (E) 125

32. QRST is a quadrilateral with TQ ┴ TS
and QR ┴ RS as shown in the figure
below. If QT = 70m, SR = 200m, and
TS = 240 m, how many square
meters are there in quadrilateral
QRST?

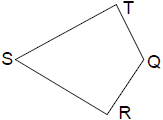
(A) 2340 (B) 16800 (C) 22400
(D) 23400 (E) 46800

33. Given line QT which goes through the
center of a circle with center C, whose
radius is 4 and P lies on the circle.
If PT = 4 and CQ =4 find the measure
of the angle x = πPQC.

(A) x < 20° (B) 20° # x < 30°
(C) 30° # x < 40° (D) 40° # x < 50°
(E)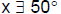

34. Two sides of a triangle are 12 cm and
8 cm, respectively. The altitude to the
12 cm side is 4 cm. Find the altitude to
the 8 cm side.

(A) 3 cm (B) 24 cm (C) 12 cm
(D) 6 cm (E) 8 / 3 cm

35. Given quadrilateral PQRS inscribed in
a circle with side PQ extended
beyond Q to point T. How many
degrees are in πTQR if πQPS = 110
degrees, & πPSR = 40 degrees?

(A) 30 (B) 70 (C) 140
(D) 40 (E) 110

36. In the figure below, AB ┴ BC,
BC ┴ CD, AB = 8, BC = 5, CD = 4.
What is the shortest distance from
A to D?

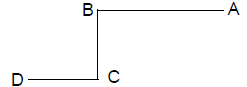
(A) 12 (B) 13 (C) 15
(D) 16 (E) 17

37. What is the effect on the volume of a
cylinder if the diameter is doubled
and the height is cut in half?

(A) the volume remains the same
(B) the volume is doubled
(C) the volume is cut in half
(D) the volume increases by a
factor of four
(E) none of these

38. What is the length of AF in this cube
that has edges 1 cm long?


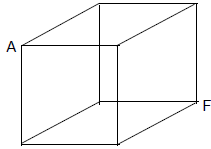
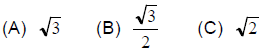
(D) 1 (E) none of these

39. A point P is selected at random on a
semicircle with diameter RS. T is the
foot of the perpendicular from P to RS.
If RS = 6 and RT = x, then the length
of PT in terms of x is:

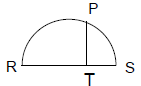
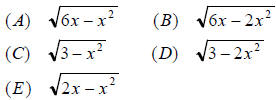
40. In the figure below, the large circle
has diameter AC. The two small
circles have their centers on AC and
are tangent to each other at the center
of the large circle. Find the area of the
shaded region, given that AC = 4.

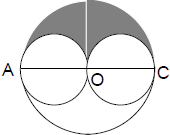
(A) 16π (B) 4π (C) 2π
(D) 1π (E) none of these