Radians,Arc Length,and Area of a Sector

The word trigonometry comes from two Greek roots, trigonon, meaning “having three
sides,” and meter, meaning “measure.” We have already defined the six basic
trigonometric functions in terms of a right triangle and the measures of its three sides.

Before beginning our study of trigonometry, we need to take a look at some basic
concepts having to do with angles.

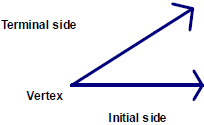
An angle is formed by two rays that share a common endpoint, called the vertex of the
angle. One ray is called initial side of the angle, and the other side is called the terminal
side. For ease, we typically will draw angles in the coordinate plane with the initial side
along the positive x axis.

We measure angles in two different ways, both of which rely on the idea of a complete
revolution in a circle.

You are probably familiar with degree measure. In this system of angle measure, we
consider that an angle which is one complete revolution is 360°. So one degree is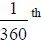
of a circle.

The second method is called radian measure. Suppose I draw a circle and construct an
angle by drawing rays from the center of the circle to two different points on the circle in
such a way that the length of the arc intercepted by the two rays is the same as the radius
of the circle. The measure of the central angle thus formed is one radian.

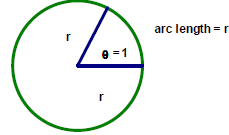
In general, the radian measure of a central angle θ can be determined by the formula
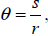where s is the length of the intercepted arc and r is the radius of the circle and r
and s are measured in the same units. A sector of a circle is the region bounded by a
central angle and the intercepted arc.

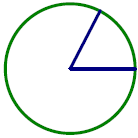
Example 1: A circle has radius 12 inches. A central angle θ intercepts an arc of length
36 inches. What is the radian measure of θ?

We know that the circumference of a circle is 2π r . In this case, the measure of the
central angle is 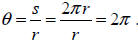So the radian measure of the central angle in the case
of a complete revolution is 2π .

Comparing the two systems, then, we have that
2π radians = 360
π radians = 180 °
π/2 radians = 90 °
etc.

As you are becoming more familiar with radian measure, you may find it helpful to be
able to convert between the two systems. We can use the statement π radians = 180 °
to help do this. Dividing both sides of that equation by π , we have that
1 radian =180°/π.

Similarly,
1 degree = π/180°.

These are the conversion formulas for radians to degrees and for degrees to radians,
respectively.

Example 2: Convert 135° to radian measure.

Example 3: Convert 4π/3 to degrees.

Example 4: Convert 2π/9 to degrees.

Example 5: Convert 18° to radian measure.

You will use some angles so often that you should know both their degree and radian
measures. These are:

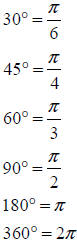
Memorize these!

Arclength and Area of a Sector
If 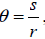 then we can multiply both sides of this equation by r, which gives us s = rθ .
This is called the arclength formula and it gives the length of the arc intercepted by the
central angle.

Example 6: If the radius of a circle is 16 inches and the measure of its central angle is
3π/4, find the arclength of the sector intercepted by the angle.

Example 7: If the arclength of a sector is 8π cm. and the radius is 12 cm., find the
measure of the central angle.

Sometimes, you’ll need to find the area of a sector. The formula for the area of a circle is
A =π r² . A sector is a fraction of a circle, determined by the measure of its central angle
over the complete revolution that is a circle, that is 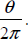So the area of a section is this
fraction of the area of the circle, that is:

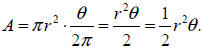
If your central angle is measured in degrees, this formula will be:

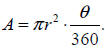
Example 8: A sector has radius 15 and central angle measuring 12.3 radians. Find the
area of the sector.

Example 9: A sector has central angle measuring 12.5 radians. The area of the sector is
2500 square units. Find the radius.