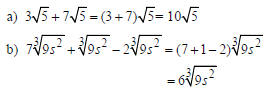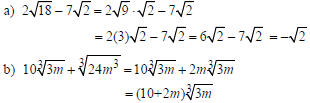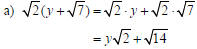Expressions Containing Several Radical Terms
| Expressions Containing Several Radical Terms
|
Adding and Subtracting Radical Expressions When two radical expressions
have the same |
| Example Simplify by combining like radical terms. 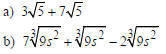 Solution
|
Example Simplify by combining like radical terms.  Solution |
| Products and Quotients of Two or More Radical Terms Radical expressions often contain factors that have more than one term. Multiplying such expressions is similar to finding products of polynomials. Some products will yield like radical terms, which we can now combine. |
Example Multiply. Simplify if possible. 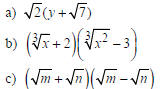 Solution
Using the |
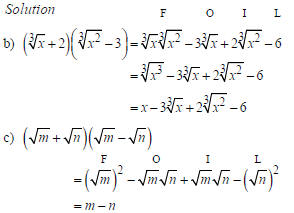 |
In part (c) of the last example, notice that the inner and outer products in FOIL are opposites, the result, m – n, is not itself a radical expression. Pairs of radical terms like, 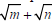 and and
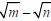 , are called , are calledconjugates. |
| Rationalizing Denominators and Numerators (Part 2) The use of conjugates allows us to rationalize denominators or numerators with two terms. |
Example Rationalize the denominator: 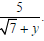 Solution 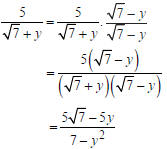 Multiplying by 1 using the conjugate |
| To rationalize a numerator with more than one term, we use the conjugate of the numerator. |
Terms with Differing Indices To multiply or divide radical terms with different indices, we can convert to exponential notation, use the rules for exponents, and then convert back to radical notation. |
| To Simplify Products or Quotients with Differing Indices 1. Convert all radical expressions to exponential notation. 2. When the bases are identical, subtract exponents to divide and add exponents to multiply. This may require finding a common denominator. 3. Convert back to radical notation and, if possible, simplify. |
Example Multiply and, if possible, simplify: 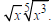 Solution 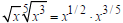 Converting to exponential notation Converting to exponential notation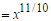 Adding exponents Adding exponents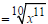 Converting to radical notation Converting to radical notation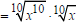 Simplifying Simplifying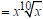 |



 Adding
and Subtracting Radical Expressions
Adding
and Subtracting Radical Expressions