Basic Linear Algebra

Linear equations form the basis of linear programming. If you have a good understanding of the
Gauss-Jordan method for solving linear equations, then you can also understand the solution of
linear programs. In addition, this chapter introduces matrix notation and concepts that will be
used in Chapters 3 and 4 (optimizing functions of several variables).

1.1 Linear Equations

The Gauss-Jordan elimination procedure is a systematic method for solving systems of linear equa-
tions. It works one variable at a time, eliminating it in all rows but one, and then moves on to the
next variable. We illustrate the procedure on three examples.

Example 1.1.1 (Solving linear equations)

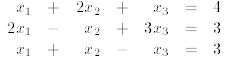
In the first step of the procedure, we use the first equation to eliminate 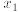from the other two.
Specifically, in order to eliminate 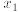from the second equation, we multiply the first equation by 2
and subtract the result from the second equation. Similarly, to eliminate 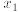from the third equation,
we subtract the first equation from the third. Such steps are called elementary row operations. We
keep the first equation and the modified second and third equations. The resulting equations are

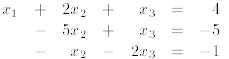
Note that only one equation was used to eliminat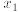e in all the others. This guarantees that the
new system of equations has exactly the same solution(s) as the original one. In the second step of
the procedure, we divide the second equation by -5 to make the coefficient of 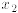equal to 1. Then,
we use this equation to eliminate 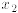from equations 1 and 3. This yields the following new system
of equations.

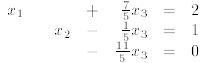
Once again, only one equation was used to eliminate 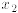in all the others and that guarantees
that the new system has the same solution(s) as the original one. Finally, in the last step of the
procedure, we use equation 3 to eliminate 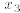  in equations 1 and 2

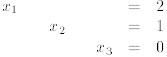
So, there is a unique solution. Note that, throughout the procedure, we were careful to keep three
equations that have the same solution(s) as the original three equations. Why is it useful? Because,
linear systems of equations do not always have a unique solution and it is important to identify
such situations.

Another example:

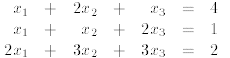
First we eliminate 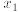from equations 2 and 3

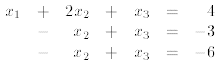
Then we eliminate 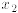from equations 1 and 3.

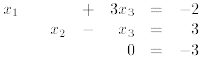
Equation 3 shows that the linear system has no solution.

A third example:

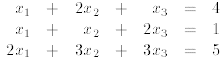
Doing the same as above, we end up with

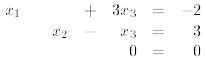
Now equation 3 is an obvious equality. It can be discarded to obtain

The situation where we can express some of the variables (here 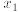and 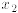) in terms of the remaining
variables (here 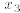) is important. These variables are said to be basic and nonbasic respectively.
Any choice of the nonbasic variable 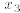yields a solution of the linear system. Therefore the system
has infinitely many solutions.

It is generally true that a system of m linear equations in n variables has either: (a) no solution, (b) a unique solution, (c) infinitely many solutions. The Gauss-Jordan elimination procedure solves the system of linear equa- tions using two elementary row operations: • modify some equation by multiplying it by a nonzero scalar (a scalar is an actual real number, such as 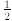or -2, it cannot be one of the variables in the problem), • modify some equation by adding to it a scalar multiple of another equation. The resulting system of m linear equations has the same solution(s) as the original system. If an equation 0 = 0 is produced, it is discarded and the procedure is continued. If an equation 0 = a is produced where a is a nonzero scalar, the procedure is stopped: in this case, the system has no solution. At each step of the procedure, a new variable is made basic: it has coefficient 1 in one of the equations and 0 in all the others. The procedure stops when each equation has a basic variable associated with it. Say p equations remain (remember that some of the original m equations may have been discarded). When n = p, the system has a unique solution. When n > p, then p variables are basic and the remaining n - p are nonbasic. In this case, the system has infinitely many solutions.

Exercise 1 Solve the following systems of linear equations using the Gauss-Jordan elimination
procedure and state whether case (a), (b) or (c) holds.

(1)

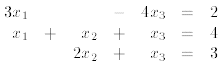
(2)

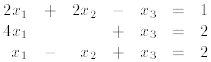
(3)

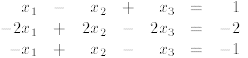
Exercise 2 Indicate whether the following linear system of equations has 0, 1 or infinitely many
solutions.

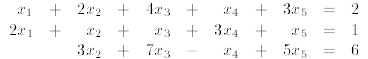
1.2 Operations on Vectors and Matrices

It is useful to formalize the operations on vectors and matrices that form the basis of linear algebra.
For our purpose, the most useful definitions are the following.
A matrix is a rectangular array of numbers written in the form

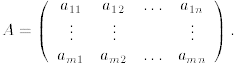
The matrix A has dimensions m × n if it has m rows and n columns. When m = 1, the matrix is
called a row vector, when n = 1, the matrix is called a column vector. A vector can be represented
either by a row vector or a column vector.

Equality of two matrices of same dimensions:

Let 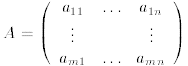and .

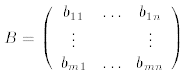Then A = B means that 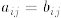for all i, j.

Multiplication of a matrix A by a scalar k:

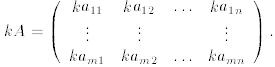
Addition of two matrices of same dimensions:

Let 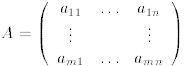and .
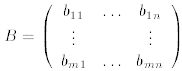Then .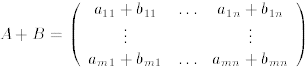

Note that A + B is not defined when A and B have different dimensions.

Exercise 3 Compute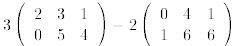

Multiplication of a matrix of dimensions m × n by a matrix of dimensions n × p:

Let 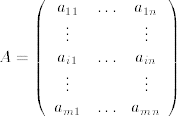and .

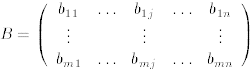Then AB is a matrix of dimensions m × p computed as follows.

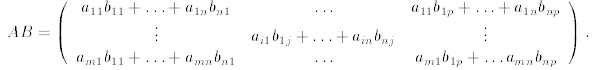
As an example, let us multiply the matrices

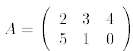and .

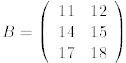The result is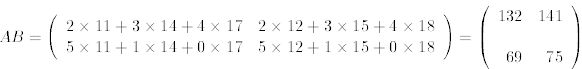

Note that AB is defined only when the number of columns of A equals the number of rows of B.
An important remark: even when both AB and BA are defined, the results are usually different.
A property of matrix multiplication is the following:

(AB)C = A(BC).

That is, if you have three matrices A, B, C to multiply and the product is legal (the number of
columns of A equals the number of rows of B and the number of columns of B equals the number
of rows of C), then you have two possibilities: you can first compute AB and multiply the result
by C, or you can first compute BC and multiply A by the result.

Exercise 4 Consider the following matrices

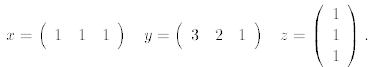
When possible, compute the following quantities:

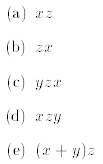
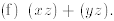
Remark: A system of linear equations can be written conveniently using matrix notation. Namely

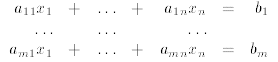
can be written as

or as

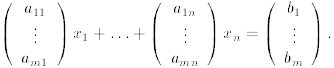
So a matrix equation Ax = b where A is a given m × n matrix, b is a given m-column vector
and x is an unknown n-column vector, is a linear system of m equations in n variables. Similarly, a
vector equation 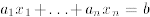where 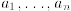, b are given m-column vectors and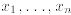
are n unknown real numbers, is also a system of m equations in n variables.