Matrix Operations
Recall how the following matrix operations are defined.
• Scalar Multiplication
When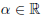 
and 
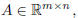then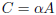 
is defined by
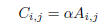for each 1 ≤ i ≤ m, 1 ≤ j ≤ n.
• Matrix Addition
When both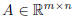 
and
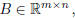then C = A + B is defined by
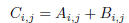for each 1 ≤ i ≤ m, 1 ≤ j ≤ n.
Note that addition is only defined when both matrices have
the same number of rows and the same number
of columns.
• Matrix Multiplication
When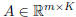 
and 
then C = AB is defined by
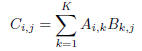for each 1 ≤ i ≤ m, 1 ≤ j ≤ n.
Note that matrix multiplication is only defined when the
number of columns of the first matrix is equal to
the number of rows of the second. Also observe that
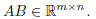
• Matrix Transpose
When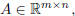 
then 
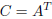is defined by
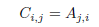or each 1 ≤ i ≤ m, 1 ≤ j ≤ n.
Note that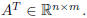 
1. Consider the following matrices.
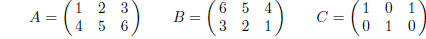
Calculate the following.
(a) A + B (b) B + C (c) − A (d) 2(A + C)
2. Consider the following matrices.
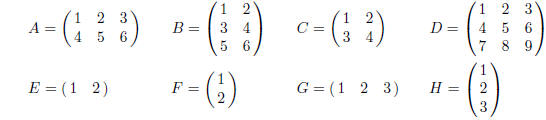
Calculate the following.
(a) AB (b) BA (c) AD (d) BC
(e) EF (f) FE (g) GH (h) HG
(i) EA (j) AH (k) EC (l) GD
3. For the matrices defined in exercise 2, compute the
following.
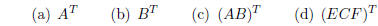
4. Given that the matrix product AB is defined, for scalar prove that
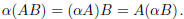
5. Given that the matrix sum A + B is defined, for scalar prove that
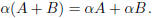
6. Given that the matrix sum A+B is defined and the matrix product CA is
defined, prove that C(A+B) =
CA + CB.
7. Given that the matrix product AB is defined, prove that
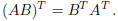
8. Let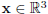 
and consider the following three
functions defined on R^3 .
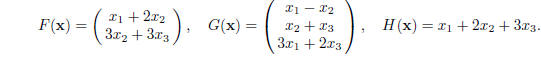
(a) F : R^3 --> what? G : R^3 --> what? H : R^3 --> what?
(b) Show all three of these functions are linear.
(c) It is possible to write each of these functions in the form of a matrix
product Mx. Explicitly determine
these three matrices.
9. Write the given systems of equations in matrix form,
i.e. y = Mx, for appropriate matrix M.
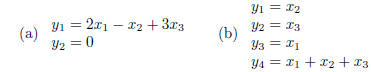
10. Consider a given matrix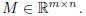 
Show the
following sets of vectors both define a vector space.
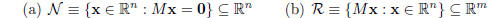
Later we will call N the null space of the matrix M, and R will be called M’s range space.