Chinese Mathematics

Here we work on worksheet #10, Guassian Elimination.

After the Han Dynasty there is a period of disorder until the Sui Dynasty from
598 to 618 A.D. But there are three very brilliant mathematicians who are active despite
the unrest. They are Liu Hui who was active in about 260 A.D., Sun Zi from the late
200’s to the 300’s A.D. and Zhu Chongzhi. (429 to 500 A.D.)

Liu Hui wrote The Sea Island Mathematical Manual and the Commentary on
the Jiuzhang Suanshu. In the latter he systematizes the presentation, provides brief ideas
of the proofs of why the calculations are valid and gives underlying principles. He uses
inscribed 96 and 192-gons to approximate the value of π. He gets π = 3.141024 (We
have 3.14159265. ) He gets close to the idea of a limit in his work on the number π. He
correctly calculated the volume of a frustrum of a square pyramid, and of a tetrahedron.
He uses the ideas in the old Chinese square root algorithm to solve equations of higher
degree. He fails to get a proof for the formula for the volume of a sphere. But his version
of the Jiuzhang Suanshu is still one that scholars use to this day.

Sun Zi wrote Master Sun’s Mathematics Manual, the Sunzi Suanjing, in
which we find the Chinese Remainder Theorem. His treatise became a standard text for
civil servants later on. The theorem is used in number theory and is often in first courses
in the subject. The Chinese used it in astronomical problem solving. For instance, at one
point in time the winter solstice, the new moon and the start of the 60-day cycle used in
ancient Chinese dating all coincided. When will this occur again? One has to reconcile
counting by 365.25’s, 29.5’s and 60’s. This would be solved by reconciling 36525, 2950
and 6000. An example shows this process better than an abstract explanation. Here is one
involving smaller numbers.

A farmer is taking as load of eggs to the local town one morning when an oxcart
accidentally bumps his basket and breaks a lot of the eggs. Luckily the farmer had his
children count the eggs before leaving home. One child remembers that she counted by
3’s as 3 is her favorite number. There were 2 eggs left over in this count. A son used the
fingers on one hand and counted by 5’s and had 3 left over. His wife used a broken egg
carton and counted by 7’s and had 2 left over. How many eggs did the farmer originally
have, so he can negotiate with the owner of the oxcart?

We write N for the number of eggs.

N = 3X + 2
N = 5Y + 3
N = 7Z + 2

First find a number that is a multiple of 5, a multiple of 7 and leaves 2 when
divided by 3. 5 x 7 = 35 which will work fine.

Secondly, find a number that is a multiple of both 3 and 5 and leaves 2 when
divided by 7. 15 is no good, but 30 works fine.

Third find a number that iis a multiple of both 3 and 7 but which leaves 3 when
divided by 5. 21 is no good, 42 is no good but 63 works fine.

So, adding the numbers we found, 35 + 30 + 63 = 128 solves the problem.

Notice however, that there are infinitely many different correct solutions to this
problem, making it what is called an indeterminate system of equations. If you add 3 x
5 x 7 = 105 to 128, or any multiple of 105, you get a perfectly satisfactory solution. So
233, 338, 443, and so on will all work. Presumably the farmer is honest, and only had
room for 128 eggs in his basket. So the number 23 = 128 – 105 also works.

Work on worksheet # 11 now, which is a Chinese Remainder Theorem
Problem.

Homework VIII

1. Given the following system of four linear equations in four unknowns, use the method
of the Jiuzhang Suanshu to find the solution.

2u - v = 0
-u + 2v - w = 0
- v + 2w - z = 0
- w + 2z = 5

2. A certain number leaves a remainder of 5 when divided by 11, a remainder of 3 when
divided by 17 and a remainder of 2 when divided by 19. Find the smallest positive
solution, and give two other solutions.

3. Use the algorithm from the Jiuzhang Suanshu to find the square root of 2 to 3 decimal
places.

The next mathematical star we study is Zhu Chongzhi, a very talented
astronomer and engineer. In addition to his mathematical achievements, he wrote 10
books in a genre that would later be called novels. He improved Liu Hui’s calculation of
π to 3.1415926 which is the same as the current 7-place approximation. He also proved
that the volume of a sphere of radius r is 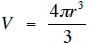, using the idea of infinitesimally
thin slices which was a method attributed to Cavalieri in Europe in the 1600’s A.D. This
is a start of the integral calculus.

The Sui Dynasty from 598 to 618 A.D. restored unity to China, engineered the
Grand Canal from the Yangtze to the Yellow River, and created a civil service system
based on merit examinations. Block printing was invented in China around 600, using
the paper that had then been in use for 500 years in China.

The more long lasting T’ang Dynasty ruled China from 619 to 907 A.D. The
civil service examination system was continued, an Imperial Academy was established
in 754. BY the late T’ang Dynasty the mathematics curriculum at the Imperial Academy
had evolved into a completed system based on the Ten Books of Mathematical Classics.
These included the Jiuzhang Suanshu, the Sea Island Mathematical Manual and Master
Sun’s Mathematical Manual. Trade with foreign nations flourished along the Silk Road
and a capital city was established at Chi’ang-an, near Xi’an. The first true porcelain
china was produced during this era. The great Chinese poet Li Po (701-762) wrote
beautiful verse in the tradition that extends back at least to the later Zhou Dynasty.

The Song Dynasty extended from 960 to 1270 A.D. This was an autocratic form
of government. During this dynasty tea, cotton and early ripening rice were harvested and
gunpowder, the magnetic compass and stern-post rudders were invented. The
mathematician Jia Xian practiced about 1050. He recognized the importance of what
we call binomial coefficients in extending the material in the fourth chapter of the
Jiuzhang Sunashu to finding roots of equations of the fourth and fifth degree. He wrote
down the array of binomial coefficients that we know in the west as Pascal’s Triangle.
Pascal studied this in 1655 A.D. We should call it Jia’s triangle, although there is
evidence of this array in Indian and Persian mathematics even before Jia. Jia created
iterative methods for solving third and fourth roots and worked with equations having
only positive coefficients.

Jia noticed the following: If one wants to solve x³ - 26, one guesses the largest
digit in the answer, say 2. Then (x + 2)³ - 26 will have the same root as the original
equation, except reduced by 2. (x - 2 + 2)³ - 26 = x³ - 26. But he expanded
(x + 2)³ - 26 as x³ + 3 (x² · 2) + 3 (x · (2)² ) + 2³ - 26 and got familiar with the
binomial coefficients for (x + h)³ and also for higher powers of x + h.

Liu Yi practiced from about 1080 to 1120 A.D. and extended Jia Xi’an’s
methods to include both positive and negative coefficients.

In 1167 A.D. the nomadic Mongols living to the north of China invaded and
conquered the Song in the north. The were led by Temujin, or Ghengis Khan.
Temujin’s grandson, Kublai Khan conquered the remaining Song empire in the south,
moved his capital to Beijing in 1264 A.D., and hosted Marco Polo from Venice from
1225 to 1292. His dynasty was called the Yuan Dynasty. Mathematics reached its
highest level of development during this time.

Four master mathematicians were active during this thirteenth century. The first
of these was Qin Jiushao (1202-1261) a brilliant, talented, athletic, womanizing
character. In 1247 he wrote a work called The Mathematical Treatise in Nine Sections.
In it he extends the Chinese remainder Theorem to work for moduli (the numbers used
like 3, 5, and 7 in the problem on the previous page) that are not necessarily relatively
prime. He introduces the use of a round zero symbol. He solves higher degree
equations, including one of degree 10. He allows positive, negative and fractional
coefficients in the equations he solves, and allows both positive and negative numbers as
solutions.

The equivalent work in our algebraic language, of the Chinese work to evaluate
higher degree polynomials and to factor them, is called synthetic evaluation and
division. The two are handled the same way. ax³ + bx² + cx + d can be
factored and written as ((ax + b)x + c)x + d. Then you calculate ax + b, multiply
by x, add c etc. Suppose we have 5x³ + 7x² - 3x -11 as our higher order polynomial.
To evaluate this polynomial for x = 2 one can organize the calculation as follows:

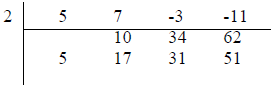(Here, bring down the 5, 2x5 =10, add, 2x17=34, add, etc.) The answer is 51

The same tabular calculation can be used to divide 5x³ + 7x² - 3x -11 by
(x – 2). You have to read the answer as

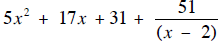
In 1248, one year after Qin Jiushao wrote the Mathematical Treatise in Nine
Sections, another gifted mathematician, Li Zhi (1192-1279) wrote The Sea Mirror of
Circle Measurements and a work called The Old Mathematics in Expanded Sections.
The first of these works consists of 170 problems having to do with the incircles and
excircles of a right triangle. These are the two circles you met in Quiz number 2. Like
Qin Jiushao he solved equations of higher degrees, using the iterative methods
generalized from the square root and cube root algorithms. He was given the same name
as the third T’ang emperor, whom he did not respect. He changed his name to Li Ye. He
was a government official in Henan Province until the Mongols overran this part of China
in 1232. He then became a scholar-hermit and lived an extremely simple life with two
friends near Fenglong Mountain. They became known as “The Friends of Fenglong
Mountain.” Kublai Khan invited, and then forced, Li Ye to accept a position in a
recognized academy, but Li Ye then got away because he was an old man. He died near
Fenglong Mountain in the city of Hebei.

The third outstanding mathematical talent during the thirteenth century in China
was Yang Hui. He lived in the south of China during the Song Dynasty. Not much is
known with certainty about his life, but he wrote “A Detailed Analysis of the
Mathematical methods in the Nine Chapters” in 1261, and a work called “The
Method of Computation of Yang Hui” in seven volumes during 1274 and 1275. His
writings consolidate what has gone before and are an important source for understanding
ancient Chinese mathematics, even today. His careful reworking of problems, and his
organizing them according to increasing degrees of difficulty brings his expositions close
to being proofs. He also gives examples of magic squares up to 10 by 10. A magic
square is a square array of numbers with the property that the sum of all of the numbers
in any column, or any row, or any diagonal, is always the same number. The oldest magic
square is the Lo Shu, dating back to at least 300 B.C.E. during the warring states period.
Legend has it that the Emperor, Yu Huang had a flood to deal with in the Yellow River
area, along a tributary called the Lo River. A turtle crawled out of the Lo River, and the
magic square called the Lo Shu was arranged on the scutes forming the shell on the back
of this turtle. The Emperor used the Lo Shu to have the flood subside. The Lo Shu is
below:

4 9 2
3 5 7The magic Number here is 15.
8 1 6

Yang numbers are odd and yin numbers are even. Chinese philosophy advises us
to strive for a balance of Yin and Yang energies in life. The 5 in the center is the average
of any two numbers on opposite sides of the 5.

We use worksheet # 12 Magic Squares at this point.

Here is a way to generate magic squares of odd order. Start with your 1 in the
top center position. Keep putting the next integer in the place to the upper right of where
you put the last number, but scrolling around, like a word processor does when you go
beyond the end of the line. So the 2 is at the bottom, and the 4 is scrolled across from the
3.

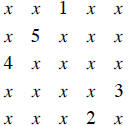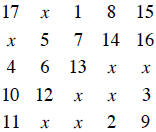One more rule. When you get stuck, like following the 5 by trying to place it
where the 1 already is, put the 6 directly under the 5, and go on. The 11 is to the upper
right of the 15 b y scrolling, so the 16 goes below the 15. Our magic number here is 65.

A famous 4x4 magic square appears in the engraving “Melancholia” by the
German artist Albrecht Durer. The year in which he created this piece of art was 1514,
the number in the bottom center of the magic square which appears on the wall behind
the perplexed angel in the engraving.

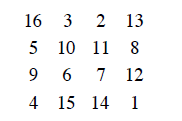
Homework IX

1. Use the wrap-around method to construct a magic square of order seven. Show
three intermediate steps. What is the magic number of this magic square?

2. a. Use the method of synthetic division to divide 3x³ - 25x² + 38x - 70 by
(x – 7). What is the answer?

b. In the above polynomial, what do you get for an answer when you substitute
x = 7?

The fourth mathematician from this century is Zhu Shijie who was most active
from about 1280 to 1303 A.D. He was respected as a mathematician and a teacher in
China. he wrote “Introduction to Mathematical Studies” for students. This text covers
all of the fields of Chinese mathematics and has the problems ordered by the degree of
difficulty. He also wrote a more advanced book with his own original contributions to
mathematics in it, called “The Jade Mirror of the Four Elements.” In this work he goes
beyond the mathematics of Qin Jiushao and Li Ye. He not only solves equations of higher
degree, but equations with up to four unknowns, say x, y, z, w. Zhu Shijie represents the
climax of mathematics and algebra in classical Chinese culture. In the ensuing centuries,
western contacts brought in more outside influences.