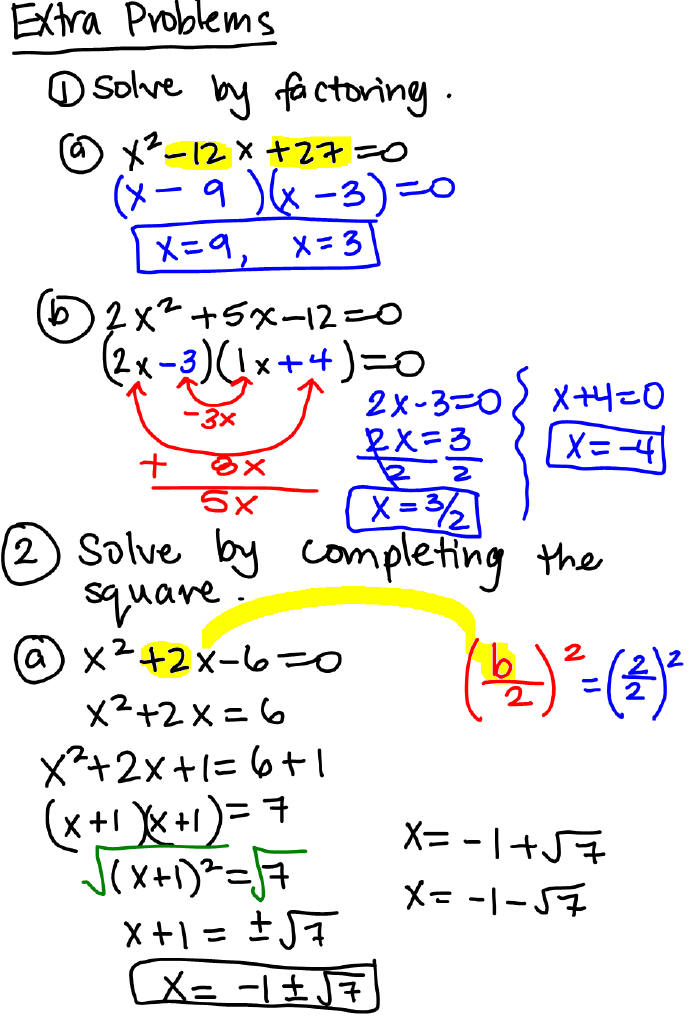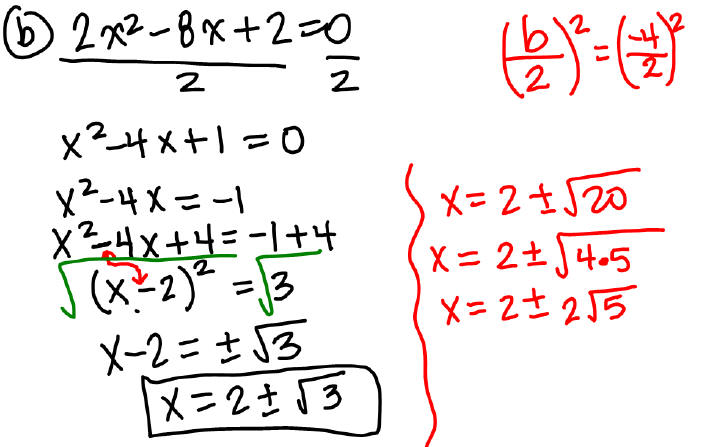Quadratic Equations
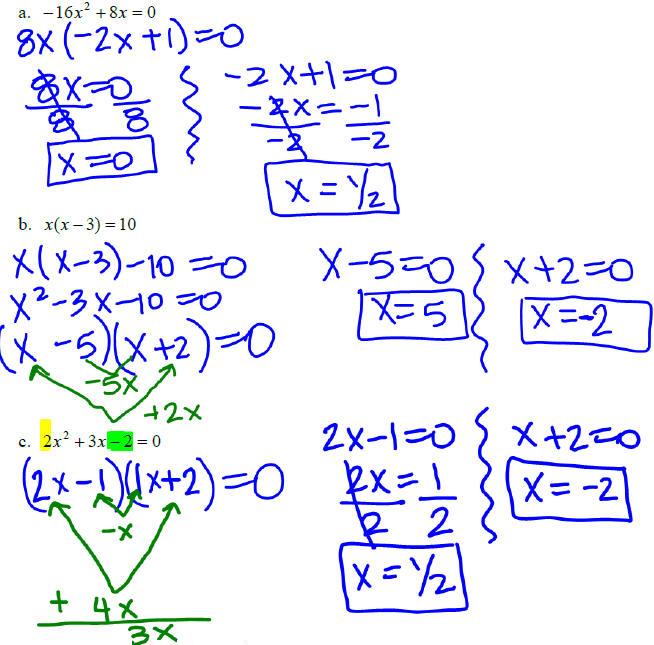
Solving by Factoring
A quadratic equation is an equation that can be written in the form
ax2 + bx + c = 0
where a, b, and c are real numbers with a ≠ 0.
To solve a quadratic equation by factoring, rewrite the
equation, if necessary, so that one
side is equal to 0 and use the Zero-Product Property:
ab = 0 if and only if a = 0 or b = 0.
Example 1: Solve the following equations by factoring.
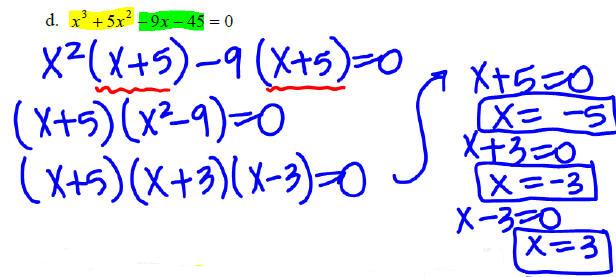
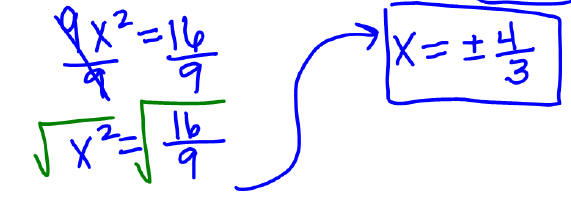
Example 2: Solve 9x2 −16 = 0 using the square root method.
Solving by Completing the Square
Given x2 + bx + c = 0
1. Rewrite the equation as x2 + bx = −c (Notice that the
leading coefficient is positive 1,
if it’s not then you will have to divide both sides of the equation by the
leading
coefficient.) and make the left –hand side a perfect square.
2. Make the left-hand side a perfect square by adding
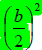 to
both sides (to balance the
to
both sides (to balance the
equation)
3. Factor the left-hand side.
4. Use the square root property to solve.
Example 3: Find all real solutions of the following
equations by completing the square.
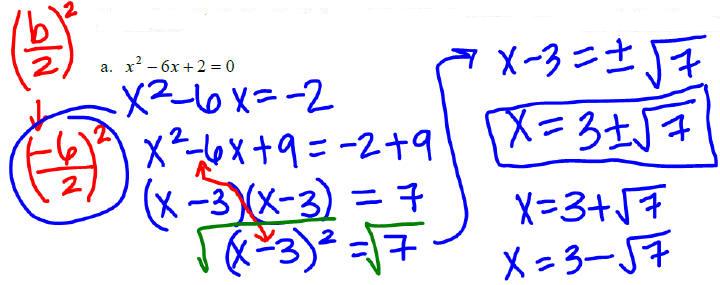
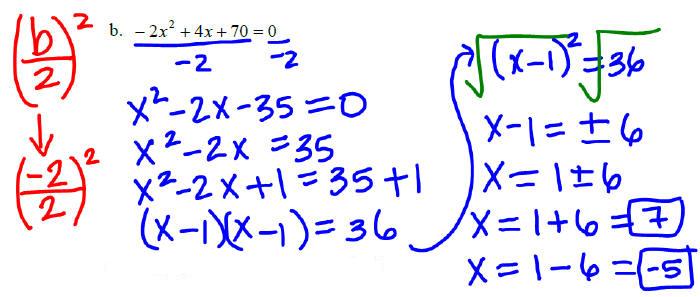
Solving by the Quadratic Formula
The solutions of the equation ax2 + bx + c = 0 , where a
≠ 0 , can be found by using the
quadratic formula:
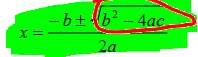
Example 4: Find all real solutions of 3x2 + 2x + 2 = 0 by using the quadratic formula.

Note: The discriminant of the equation ax2 + bx + c = 0 ( a ≠ 0) is given by
D = b2 − 4ac .
If D > 0, then the equation ax2 + bx + c = 0 has two
distinct real solutions.
If D = 0, then the equation ax2 + bx + c = 0 has exactly one real solution.
If D < 0, then the equation ax2 + bx + c = 0 has no real solution (The roots of
the
equation are complex numbers and appear as complex conjugate pairs.)