Princeton University MATH 202

FEB 15, 2008

i. Some stuff I forgot to mention last time

Two notations for linear transformations of the plane: we write



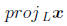
for projection onto the line L. If u is a unit vector of L, then



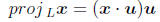
We write



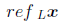
for reflection about the line L. So again, using u to denote a unit vector of L, we have



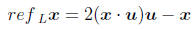
ii. Inverse of a linear transformation

• First, recall the inverse of a function/transformation/map

– (Draw standard picture with sets and maps.)

– Remember that a transformation (or a map) is an association between two sets, X, the
domain, and Y , the codomain, with every elements in X associated to an image.

– A transformation is invertible if the association can go the other way, i.e., every element
in Y is the image of only one element in x.

– There are two ways for a transformation to fail to be invertible: 1) not every element
in the codomain is the image of an element in the domain (give example) or 2) some
element in the codomain is the image of more than one element in the domain (give
example).

– If the transformation T : X → Y is invertible, we write T^-1 to denote the inverse
transformation defined from Y → X. For every y = T(x), we have that T^-1(y) = x.
In other words, T^-1(y) is the one and only one x ∈ X satisfying T(x) = y.

– We have

T(T^-1(y)) = y , T^-1(T(x)) = x

– If T is invertible, T^-1 is also invertible, with

(T^-1)^-1 = T

– Example: T : R → R,

T(x) = x³

is invertible. Neither of the possible points of failure are problems.

– Example:

T(x) = x³ − x²

is not invertible. It fails the second possible point of failure: the points 0, 1 both satisfy
T(0) = 0 and T(1) = 0. So 0 ∈ Y is an example of a point that does not have a unique
pre-image in X.

– Definition: given a transformation T : X → Y , the pre-image of a point y ∈ Y is the
set of all points X ∈ X with T(x) = y. So the criteria for T to be invertible is that
every element in Y has one and only one pre-image.

– Example: T : R → R

T(x) = x²

fails both criteria: T(x) = T(−x), so every positive number has two pre-images. On
the other hand, every negative image has no pre-image.

– Fact: if the transformation only fails the first criteria, i.e., if there exists y such that the
pre-image of y is empty, but for every element y with a pre-image, the pre-image is
unique, then we can make the transformation invertible if we shrink the codomain to
remove all the extra points.

– For example, if we consider T(x) = x² as a map from the positive real numbers to
itself, then T is invertible.

• Now, let’s restrict our attention to linear transformations. Remember that the linear transformation
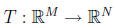can be associated to an N ×M matrix A. We consider whether T is
invertible by the dimension of A.

– N > M: if N > M, the rref of the coefficient matrix A must have rows in the bottom
that consist of all zeros. (Remember, the number of pivots/dependent variables of A is
at most M. Since N > M, there must be rows without pivots. And so they have to
be all zero.) So, if we choose b carefully in the beginning, the rref of the augmented
matrix can be made (for good choices of b) to have a row that looks like



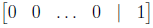
and therefore is inconsistent. This means that we can find b ∈ such that there is no
solution to

Ax = b

which means that the linear transformation T fails the first criterion for invertible.
– N < M: if N < M, remember that we showed last Friday that

Ax = b

has either zero or infinite solutions for every single b (since there must be free parameters).
So the linear transform cannot be invertible (it must fail at least one of the
criteria).

– N = M: if N = M, remember that the system

Ax = b

has a unique solution if and only if the rank of A is equal to M. This in particular
means that the linear transformation T is invertible if the rref of its associated matrix
A is the identify matrix I_M.

• Question: of the five transformations onWednesday (scaling, projection, reflection, rotation,
shear), which are invertible?

• Now, if T is a linear transformation, and T is invertible, then T^-1 is also a linear transformation.
(Since T takes lines to lines and the origin to the origin, and does so uniquely, the
pre-image of a line is still a line, and the pre-image of the origin is still the origin...)

• The criteria for a linear transformation T : → to be invertible can be simplified.
Notice that for any linear transformation

A0 = 0

using linearity, we only need to check to see whether the 0 vector is the unique vector with
Ax = 0, i.e., for the linear transformation given by a square matrix, the matrix is not invertible
if and only if there are infinitely many solutions to Ax = 0.

• Since T^-1 is a linear transformation, it has an associated matrix. We write it as A^-1, and call
it the inverse matrix of A.

• A square matrix A is said to be invertible if its associated linear transformation T is invertible.
And its inverse matrix is A^-1. (We restricted to square matrices since we have already
seen that non-square matrices cannot have linear transformations that are invertible.)

• What does it mean for T to be invertible? Consider the system of equations

Ax = y

if A is invertible, we can write

x = A^-1y

i.e., we can solve for x uniquely in terms of y.

• How to find the inverse? Example: is the matrix

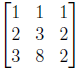
invertible, and what is its inverse? (Show the diagonalization process.)

• This process can be succintly described as doing Gauss-Jordan elimination on the M × 2M
matrix

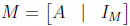
A is invertible when



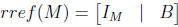
for some B, and in this case A^-1 = B. If, on ther other hand, the left half of rref(M) fails
to be I_M, then A is not invertible. (Notice that the left half of rref(M) is rref(A).)

• Example:

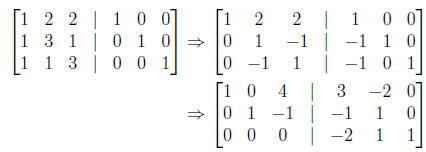
So the matrix is not invertible

• Example:

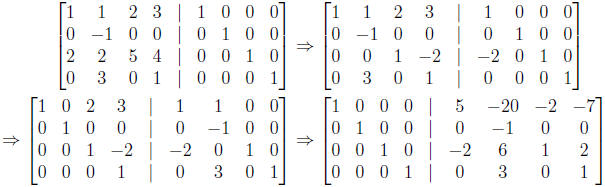
and the matrix is invertible with the inverse given.

• Example: for which k is the following invertible?

We don’t need to compute the full M × 2M matrix since we are only asking about invertibility,
and not about finding the actual inverse. So all we need to look for is whether the rref
is equal to the identity matrix. In this case, as long as 9−2k ≠ 0, we can divide the last row
by 9 − 2k and finish the Gauss-Jordan elimination to get the identity matrix. So if 9 − 2k is
not 0, the matrix is invertible. On the other hand, if 9 − 2k is 0, the above matrix is in rref,
and so the matrix is not invertible.
• Formula for 2 × 2 matrices. Start with .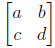

– If a, c are both 0, then the matrix is not invertible: since G-J can never give you a
leading 1 in the first column. So we can assume that at least one of a and c is non-zero.
Since G-J allows swapping of rows, we can assuming that a is non-zero.
– Then divide the first row by a. And continue with G-J

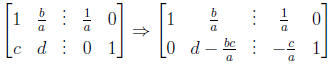
So as long as the quantity 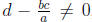, we can continue the G-J elimination. Since
a ≠ 0, we multiply the relation and write it as ad − bc ≠ 0. Notice that in the case
where a = c = 0, this quantity ad−bc is also 0. This means that as long as ad−bc ≠ 0,
we can continue all the way past this step.

– Then we finish the G-J

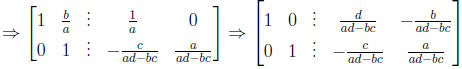
– The quantity ad − bc is called the determinant of the matrix. Suppose the matrix
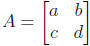, we write det(A) = ad − bc.

– Conclusion: given a 2 × 2 matrix .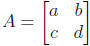

*  A is invertible if and only if its determinant det(A) = ad − bc ≠ 0.
*  and when A is invertible its inverse is



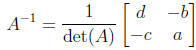
HOMEWORK FOR THIS WEEK

2.1: 4, 6, 10, 19, 20, 35

2.2: 4, 10, 12, 36

2.3: 10, 20, 26, 30, 35