Numerical Linear Algebra Background
• matrix structure and algorithm complexity
• solving linear equations with factored matrices
• LU, Cholesky, LDLT factorization
• block elimination and the matrix inversion lemma
• solving underdetermined equations
Matrix structure and algorithm complexity
cost (execution time) of solving Ax = b with A ∈ Rn×n
• for general methods, grows as n3
• less if A is structured (banded, sparse, Toeplitz, . . . )
flop counts
• flop (floating-point operation): one addition,
subtraction,
multiplication, or division of two floating-point numbers
• to estimate complexity of an algorithm: express number
of flops as a
(polynomial) function of the problem dimensions, and simplify by
keeping only the leading terms
• not an accurate predictor of computation time on modern computers
• useful as a rough estimate of complexity
vector-vector operations (x, y ∈ Rn)
• inner product xT y: 2n -1 flops (or 2n if n is large)
• sum x + y, scalar multiplication x: n flops
matrix-vector product y = Ax with A ∈ Rm×n
• m(2n - 1) flops (or 2mn if n large)
• 2N if A is sparse with N nonzero elements
• 2p(n + m) if A is given as A = UVT , U ∈ Rm×p, V ∈ Rn×p
matrix-matrix product C = AB with A ∈ Rm×n, B ∈ Rn×p
• mp(2n - 1) flops (or 2mnp if n large)
• less if A and/or B are sparse
• (1/2)m(m + 1)(2n - 1) ≈ m2n if m = p and C symmetric
Linear equations that are easy to solve
diagonal matrices
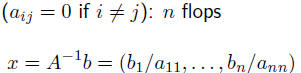
lower triangular
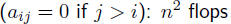
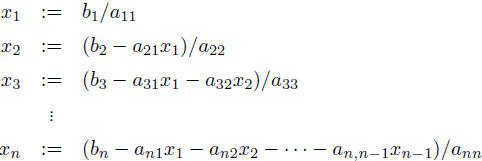
called forward substitution
upper triangular 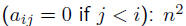 flops via backward substitution
flops via backward substitution
orthogonal matrices: A-1 = AT
• 2n2 flops to compute x = AT b for general A
• less with structure, e.g., if A = I - 2uuT
with
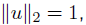 we can
we can
compute x = AT b = b - 2(uT b)u in 4n flops
permutation matrices:
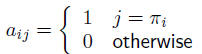
where 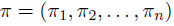 is a permutation
of (1, 2, . . . , n)
is a permutation
of (1, 2, . . . , n)
• interpretation:
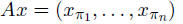
• satisfies A-1 = AT , hence cost of
solving Ax = b is 0 flops
example:
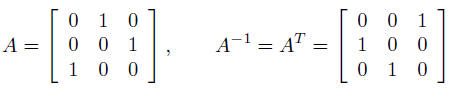
The factor-solve method for solving Ax = b
• factor A as a product of simple matrices (usually 2 or
3):
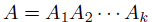
(Ai diagonal, upper or lower triangular, etc)
• compute 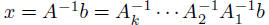 by solving k ‘easy’ equations
by solving k ‘easy’ equations
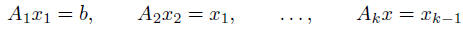
cost of factorization step usually dominates cost of solve step
equations with multiple righthand sides
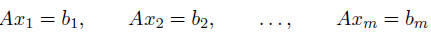
cost: one factorization plus m solves
LU factorization
every nonsingular matrix A can be factored as
A = PLU
with P a permutation matrix, L lower triangular, U upper
triangular
cost: (2/3)n3 flops
given a set of linear equations Ax = b, with A nonsingular.
1. LU factorization. Factor A as A = PLU ((2/3)n3 flops).
2. Permutation. Solve 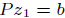 (0 flops).
(0 flops).
3. Forward substitution. Solve 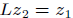 (n2
flops).
(n2
flops).
4. Backward substitution. Solve 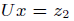 (n2
flops).
(n2
flops).
cost: (2/3)n3 + 2n2 ≈ (2/3)n3
for large n
sparse LU factorization
A = P1LUP2
• adding permutation matrix P2 offers
possibility of sparser L, U (hence,
cheaper factor and solve steps)
• P1 and P2 chosen (heuristically) to yield sparse L, U
• choice of P1 and P2 depends on sparsity pattern and values of A
• cost is usually much less than (2/3)n3; exact
value depends in a
complicated way on n, number of zeros in A, sparsity pattern
Cholesky factorization
every positive definite A can be factored as
A = LLT
with L lower triangular
cost: (1/3)n3 flops
given a set of linear equations Ax = b, with
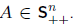
1. Cholesky factorization. Factor A as A = LLT ((1/3)n3
flops).
2. Forward substitution. Solve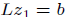 (n2
flops).
(n2
flops).
3. Backward substitution. Solve 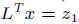 (n2
flops).
(n2
flops).
cost: (1/3)n3 + 2n2 ≈ (1/3)n3 for large n
sparse Cholesky factorization
A = PLLTPT
• adding permutation matrix P offers possibility of sparser L
• P chosen (heuristically) to yield sparse L
• choice of P only depends on sparsity pattern of A (unlike sparse LU)
• cost is usually much less than (1/3)n^3; exact value
depends in a
complicated way on n, number of zeros in A, sparsity pattern
LDLT factorization
every nonsingular symmetric matrix A can be factored as
A = PLDLTPT
with P a permutation matrix, L lower triangular, D block
diagonal with
1 × 1 or 2 × 2 diagonal blocks
cost: (1/3)n3
• cost of solving symmetric sets of linear equations by
LDLT factorization:
(1/3)n3 + 2n2 ≈ (1/3)n3 for large n
• for sparse A, can choose P to yield sparse L; cost ≪ (1/3)n3
Equations with structured sub-blocks
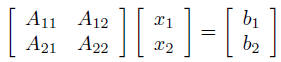 (1)
(1)
• variables 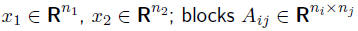
• if A11 is nonsingular, can eliminate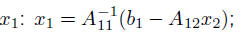
to compute x2, solve
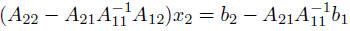
given a nonsingular set of linear equations (1), with A11
nonsingular.
1. Form 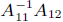 and
and 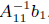
2. Form 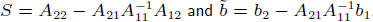
3. Determine x2 by solving 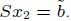
4. Determine x1 by solving 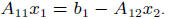
dominant terms in flop count
• step 1: 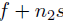 (f is
cost of factoring A11; s is cost of solve step)
(f is
cost of factoring A11; s is cost of solve step)
• step 2: 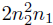 (cost
dominated by product of A21 and
(cost
dominated by product of A21 and 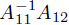 )
)
• step 3: 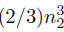
total: 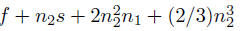
examples
• general 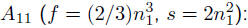 no gain over
standard method
no gain over
standard method
#flops 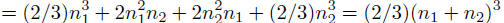
• block elimination is useful for structured
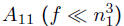
for example, diagonal 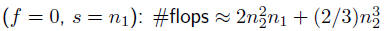
Structured matrix plus low rank term
(A + BC)x = b
• A ∈ Rn×n, B ∈ Rn×p, C ∈ Rp×n
• assume A has structure (Ax = b easy to solve)
first write as
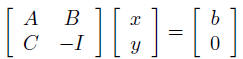
now apply block elimination: solve
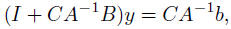
then solve Ax = b − By
this proves the matrix inversion lemma: if A and A + BC
nonsingular,
(A + BC)-1 = A-1 - A-1B(I + CA-1B)-1CA-1
example: A diagonal, B,C dense
• method 1: form D = A + BC, then solve Dx = b
cost: (2/3)n3 + 2pn2
• method 2 (via matrix inversion lemma): solve
(I + CA−1B)y = CA-1b, (2)
then compute x = A-1b - A-1By
total cost is dominated by (2): 2p2n + (2/3)p3 (i.e.,
linear in n)
Underdetermined linear equations
if A ∈ Rp×n with p < n, rank A = p,
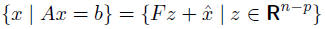
• 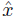 is (any) particular
solution
is (any) particular
solution
• columns of 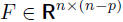 span nullspace of A
span nullspace of A
• there exist several numerical methods for computing F
(QR factorization, rectangular LU factorization, . . . )


