Quadratic Fit

Here is a definition of a linear function f :



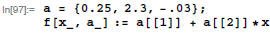
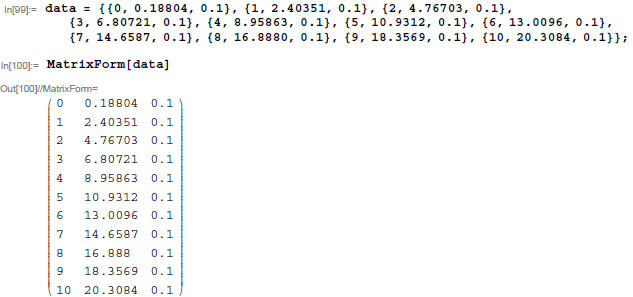
Now generate a data set in list named "data."

The "x" values are in data[[i,1]] (column 1 below), the "measured" y values are in data[[i,2]] (column 2 below), and the uncertainties
in the y values are in data[[i,3]] (column 3 below).

Convert one of the next three cells from "text" format to "input" format to fill the list named "data." The first cell generates a data
set based on a quadratic function with random noise; the second cell imports the data from a file named "sample.dat"; the third
uses the sample data from from the writeup.

data = Table[{x = i,f[x,a]-0.3 x^2 +Random[NormalDistribution[0,.1]],.1},{i,0,10}];

data=Import["sample.dat"]

Separate the list "data" into a list that has x-y pairs only ("xydata"), and a list that has the weights for each point ("w"). This is
convenient for the Mathematica syntax in the function Regress below.

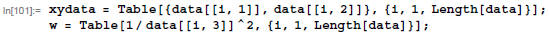
Export["example3.dat",testdata]; (* Export data for gnuplot comparison if desired *)

Define functions that calculate x² . The function x² includes weights; the function x² nw doesn't.

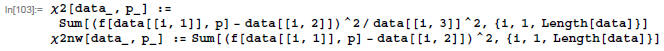
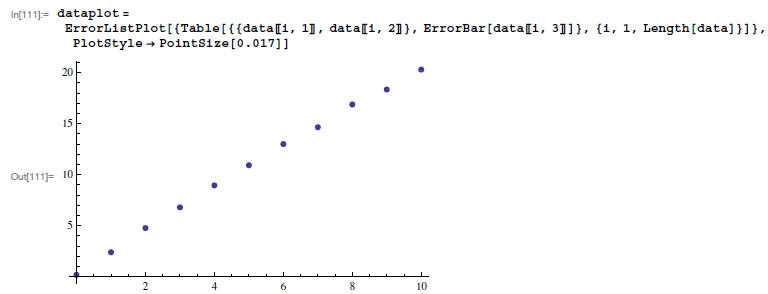
  Minimize x² with weighted LINEAR fitting

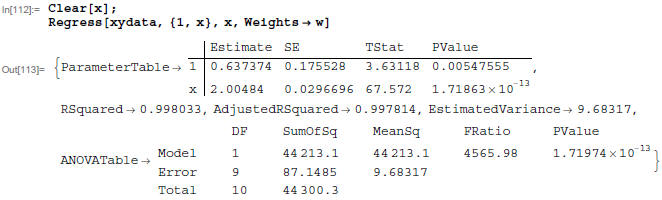
You can get other specific information in the RegressionReport that is the output of the Regress function. Note that the Covariance-
Matrix of Mathematica is the curvature matrix, α , TIMES the reduced x² of the original data set.. (See my notes and
error_test.nb)

To use information from RegressionReport, I give the rules returned in the RegressionReport a name, and then I given pick out the
individual information:

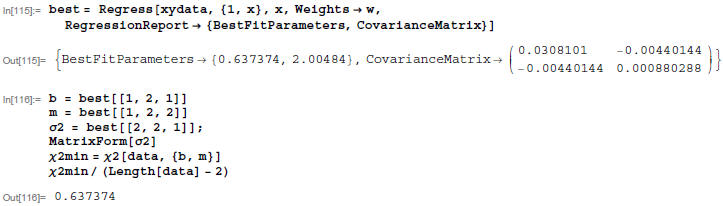
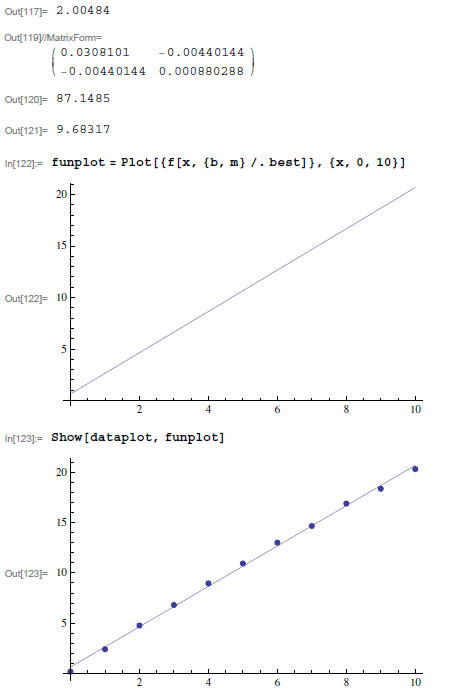
This plot looks linear, but the value of the reduced x² is pretty high. Let's plot residuals:

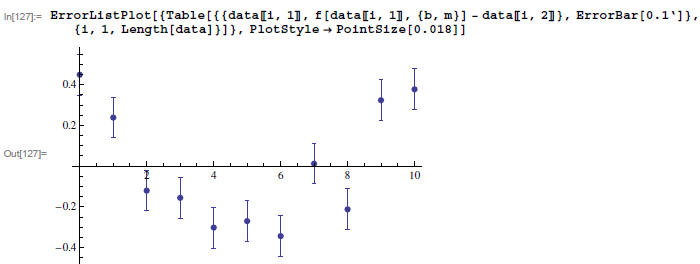
This suggests that there a quadratic term might be a good thing in our fitting function.

Redo with weighted QUADRATIC fitting

Add a term to the function f to make it a quadratic:

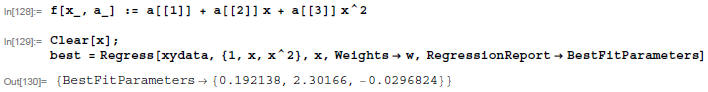
To use information from Report:

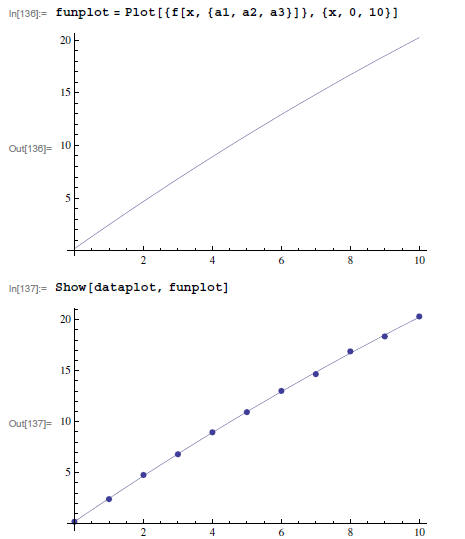
Plot residuals:

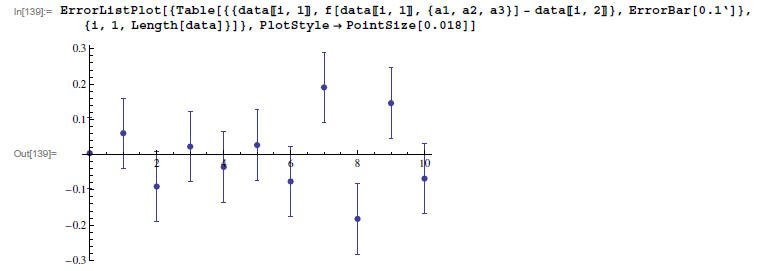
MUCH BETTER!

Using Calibration

Assume that you measure some value of y, and call this value Y, with uncertainty ΔY.

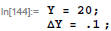
The following gives the best X (you could use quadratic formula to find X in this case):

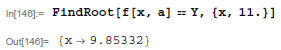
Generate hypothetical data sets

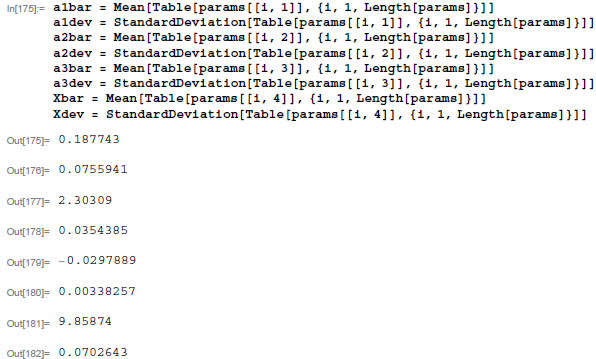
NOTE: The final uncertainty Xdev is due to uncertainty in parameters and uncertainty Δ Y. You can check relative contributions
by fixing hY = Y and recalculating to give uncertainty due to parameters, and using linear approx to get uncertainty due to Δ Y:

(Δ X)_{parameter unnertainty} = 0.041

(Δ X)_{Y uncertainty} = Δ Y/(local slope) = .1/(2.3 - .06 \times X) = 1.71 = 0.058

(Δ X)_total = Sqrt[.0041^2 + 0.058^2] = 0.071