Optimum Design of Mechanical Elements and Systems

Problem 1: For the following functions:

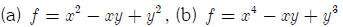
find the Taylor series about (1,1) up to quadratic term. Then, using the Taylor series,
predict the function value at (1.1, 0.8). Compare against exact value.

Problem 2: For the generic quadratic function:

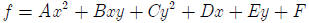
classify the stationary point (minimum, maximum, saddle, 'other') based on the
coefficients. Using this general expression, classify the stationary points of

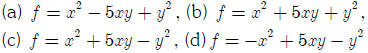
Problem 3: For the following quadratic functions:

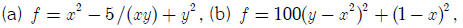
find the stationary point(s) (using MATLAB's ezmesh, ezcontour, fminunc, …), and
classify.

Problem 4: Consider the function:

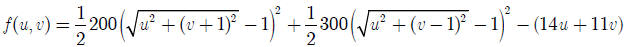
Find the minimum using fminunc. Now find the minimum within the region
0 < u < 0.5 and 0 < v < 0.1 using a naïve random search using K = 1,00,0000
(maximum) random searches. Plot the error (distance from exact to result from
random search) for K =100, K =1000, K = 10000, K = 100,000 and K =
1,00,0000. There is no need to submit your Matlab code; just submit the plot.

Problem 5: Consider the function f (x,y) = 3x^2−xy + 4y^2−x −y . Find the
minimum by performing line-search in two directions, first in x then in y, starting at
(0,0). (You need to do this problem by hand, but you are welcome to confirm your
answers with the line-search code.)

Problem 6: Consider the function f (x,y) = x^2 −xy + 4y^2 + x −3 . Suppose a
direction d = (1,1) is given. Find the corresponding conjugate direction. Using this
pair show that you can find the minimum from the origin in two steps.

Problem 7: Write a Matlab function to find the minima of an arbitrary N-D function
via the Powell's method (you may use the line-search method provided, but at your
own risk!). Your code should be of the form:

function [xMin,fMin,iter] = ...

Powell_LastName(f,xBar0,xTol,fTol,maxIterations)

where the function parameters are as before. Test your code against a variety of
quadratic and non-quadratic functions. Email only the Powell code (and not the test scripts).