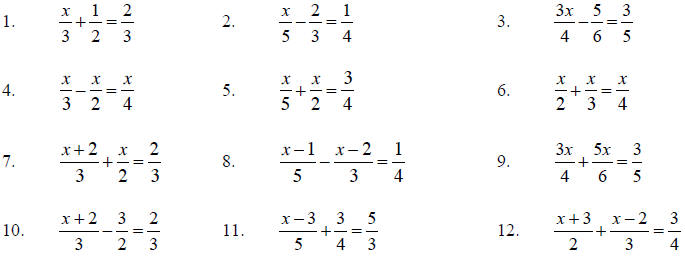Algebraic Expression
1.3 Linear Equations
An equation is two expressions that are equal (same).
equal =>" = "
Examples
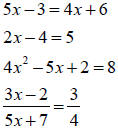
Linear equations have linear expressions.
Examples
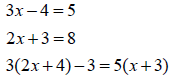
More Algebraic Properties
Identity Property
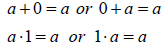
| Examples | Examples |
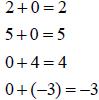 |
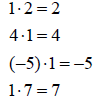 |
Inverse Property
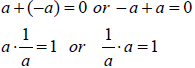
| Examples | Examples |
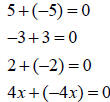 |
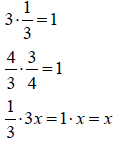 |
Equation Properties
Addition/Subtraction property of equality
If a =b then
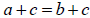
If a =b then
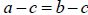
Multiplication/Division property of equality
If a =b then
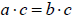 |
Note : c ≠ 0 |
If a =b then
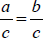 |
Using the inverse property with the equality properties,
we can solve basic equations.
Example
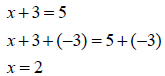 or
or
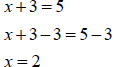 or
or
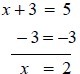 |
Example
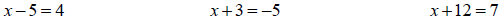
Example
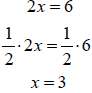 or
or
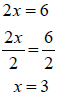
Example
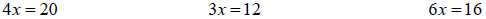
Example

When we have multiplication and addition in a problem.
Example
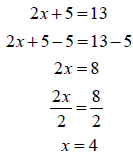 or
or
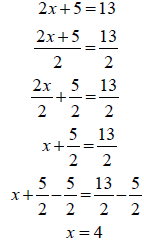 |
Note: |
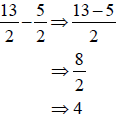 |
Which seems easier?
Examples
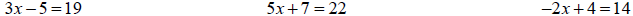
Examples

Before moving terms, we should simplify the expressions
first.
Examples

Solving
1. Simplify each side of the equation.
2. Move terms by adding or subtracting
3. Divide by the coefficient
Examples

Homework:
Solve the equations.
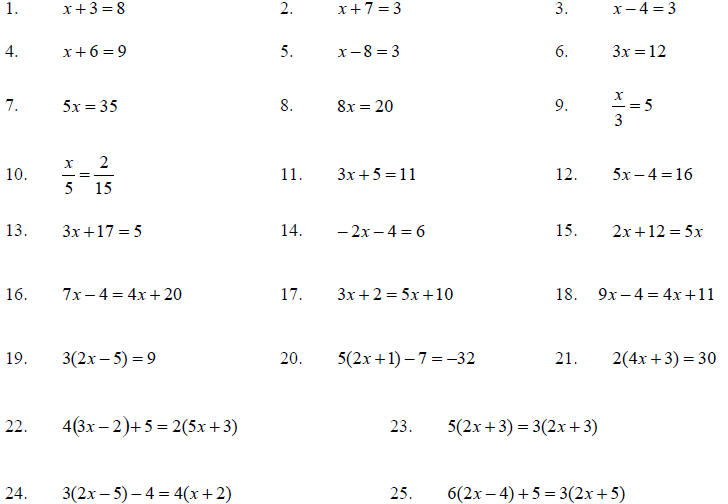
1.4 Eliminating Denominators
Fraction:
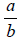
What is the operation for the fraction?
What is the inverse operation?
To eliminate denominators, we multiply by a common denominator.
A common denominator (C.D.) can be found by multiplying the different
denominators
together. Note: This may not be the least common denominator.
Example
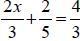
Different denominators :3 and 5
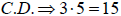
multplying both sides by the C. D.
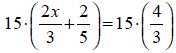
Distributing
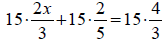
Simplifying
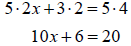
Now solve the linear equation
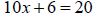
| Example | Example |
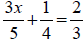 |
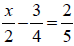 |
| Example | Example |
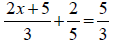 |
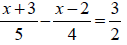 |
Homework: